Uma série temporal é a sequência ordenada de valores de uma variável em intervalos de tempo igualmente espaçados, sendo considerada univariada quando consiste de observações únicas (escalares). A análise de séries temporais leva em conta o fato que os pontos de dados tomados no decorrer do tempo possam ter uma estrutura interna (tal como correlação, tendência ou variações sazonais) que deverá ser considerada. As séries são muito utilizadas para entender as forças e estruturas que geraram os dados observados, assim como ajustar um modelo matemático que permita o monitoramento e a previsão da variável de interesse.
Foi criado um script em R para fazer algumas das principais análises de séries temporais, incluindo a relação entre duas (ou mais) delas. O script está disponível no GitHub/ts_analysis, sendo que a explicação de parte do código vem nos itens a seguir. Todos os gráficos são impressos em um arquivo PDF para cada série temporal e todos os resultados de testes e valores são impressos na tela, mas podem ser redirecionados para um arquivo ao executar o script no terminal Linux.
Os dados utilizados como exemplo são médias mensais de concentração de CO2 (em ppm) desde 1960 registradas em Mauna Loa, Havaí, baixados no site Scripps CO2 Program e de preços do barril de petróleo cru (em dólares) nos EUA desde 1974, baixados do site eia (variável regressora, usada somente no final do texto). As datas e valores foram reorganizadas no modelo “YYYY-MM-DD,FFF.FF” (colunas “date” e “value”) e utilizadas somente no intervalo em comum entre as duas séries: de 1974-01-01 a 2015-12-01. O período entre 2015 e 2017 (aproximadamente 10% da série) foi reservado para uma estatística de acurácia no final do post.
Embora um conjunto de dados de uma série temporal univariada seja geralmente dado como uma única coluna de números, o tempo é uma variável implícita. Se os dados estão igualmente espaçados, a variável tempo (ou índice) não precisa ser dada explicitamente. A variável tempo pode algumas vezes ser explicitamente usada para plotar a série, mas não é usada no modelo de série temporal em si. A conversão de uma tabela com data e valores para um objeto do tipo “time serie” é feio através da função ts() do R.
Um dos primeiros passos é avaliar a existência de outliers, que são valores atípicos e inconsistentes com o restantes da série. Isso pode ser efetuado visualmente no gráfico da série em função do tempo, de resíduos e de um histograma. De modo geral, esses pontos atípicos podem ser excluídos (o script vai fazer uma interpolação para manter a série com intervalo constante, substituindo onde estiver “-99.99”), mas é interessante investigar separadamente a causa desses outliers.
Tendência e sazonalidade
Uma série temporal pode ser decomposta nos seguintes itens (com nome em inglês entre parênteses):
- Tendência (trend) – elementos de longo prazo relacionados com a série de tempo (pode ser constante, descer ou ascender com o tempo)
- Ciclo – ondas longas, mais ou menos regulares, em torno de uma linha de tendência
- Sazonalidade (seasonal) – ondas curtas, padrões regulares da série de tempo, flutuações periódicas
- Aleatório (random) – todos os efeitos que não foram incorporados pela série de tempo via os três componentes anteriormente citados, ou seja, é o resíduo
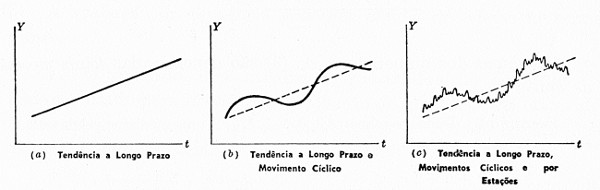
Essas componentes podem se somar ou se multiplicar para formar a série temporal (modelo aditivo ou multiplicativo, respectivamente). O modelo aditivo é útil quando a variação sazonal é relativamente constante ao longo do tempo, enquanto que o multiplicativo é usado quando a variação sazonal aumenta ao longo do tempo.
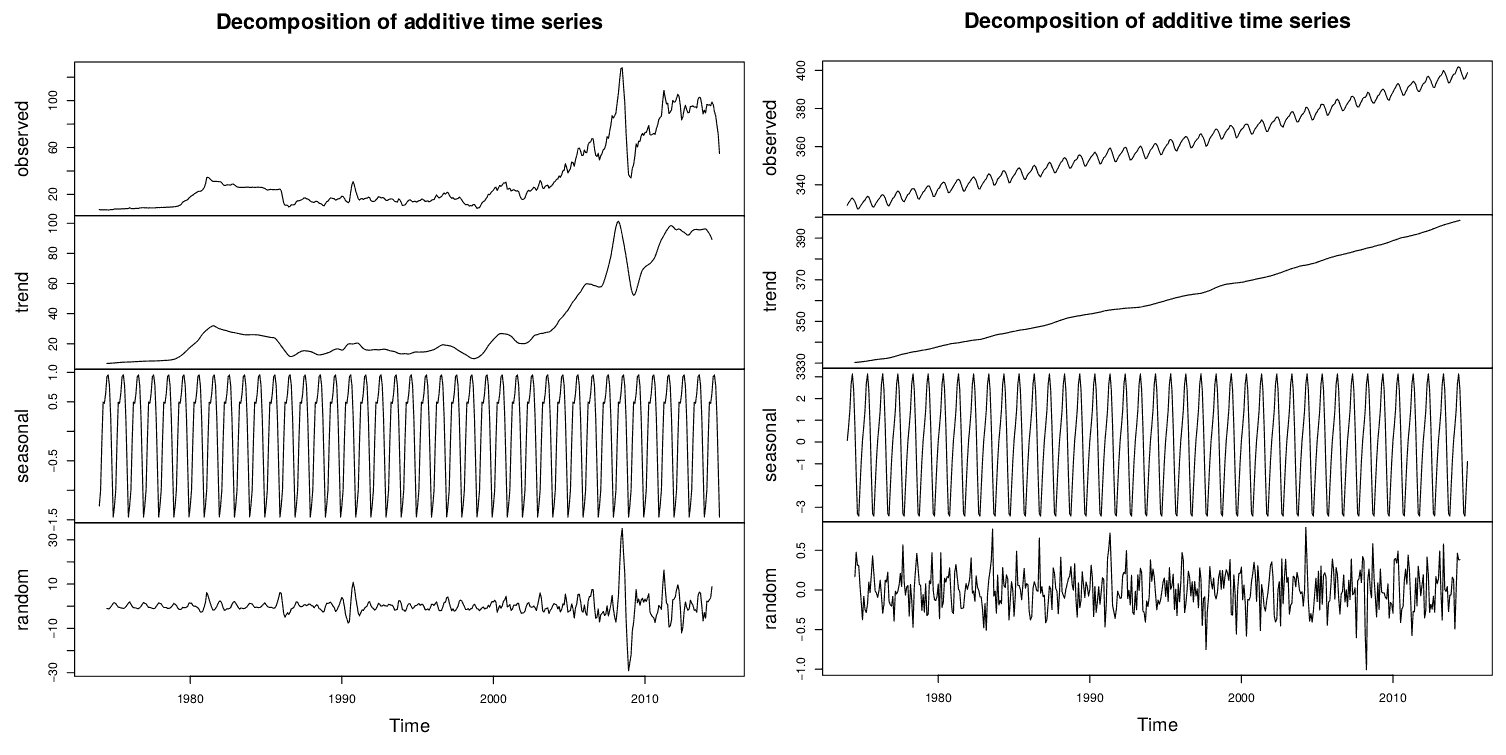
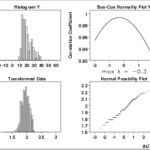
O R possui a função decompose(), que decompõe as componentes da série temporal em gráficos alinhados no tempo. Desse modo, é possível verificar se existe tendência e sazonalidade, assim como analisar a componente de dados aleatórios (sem tendência/sazonalidade). Os valores dessa série sem tendência nem sazonalidade devem ter distribuição normal, o que pode ser facilmente observado através de um histograma – veja mais no post sobre Teoria dos Erros. Essa série ainda pode receber uma transformação, como a de Box-Cox, para normalizar sua distribuição.
Além da análise gráfica, existem testes para verificar se existe tendência, como os testes de Wald-Wolfowitz (ou “runs test”), de Cox-Stuart e de Mann-Kendall, e para verificar se existe sazonalidade, como os testes de Kruskal-Wallis e de Friedman. Mais informações dos testes no post Testes de tendência e sazonalidade.
A saída completa dos testes para as duas séries temporais do exemplo podem ser vistas no GitHub (arquivo output_tests.txt). Em todos os casos, deve-se rejeitar a hipótese alternativa de não-aleatoriedade (ou seja, provavelmente existe tendência).
No teste de Kruskal-Wallis, não é possível rejeitar a hipótese nula de que todas as populações possuem funções de distribuição iguais. Já no teste de Friedman, devido ao p-valor muito pequeno, rejeita-se a hipótese nula de que não existe sazonalidade determinística, ou seja, é muito provável que exista sazonalidade.
Obs.: o “p-valor” (ou p-value) é a probabilidade de se obter uma estatística de teste igual ou mais extrema que aquela observada em uma amostra. Ou seja, um p-valor pequeno significa que a probabilidade de obter um valor da estatística de teste como o observado é muito improvável, levando assim à rejeição da hipótese nula. Veja mais sobre o p-valor no post sobre Testes de Hipóteses.
Estacionariedade
Um processo estacionário tem a propriedade de que a média, variância e estrutura de autocorrelação não mudam no decorrer do tempo – ou seja, não possui tendência nem sazonalidade. É possível verificar essa propriedade através da visualização do gráfico da variável em função do tempo ou também através de testes como Dickey-Fuller Aumentado (ADF), Phillips-Perron (PP) e KPSS – mais informações no post Processos Estacionários.
A saída completa dos testes para as duas séries temporais do exemplo podem ser vistas no GitHub (arquivo output_tests.txt). Nos três casos, comparando-se com os valores críticos tabelados, a hipótese nula de uma raiz unitária será rejeitada (pouco provável ser estacionário).
Para retirar a tendência de uma série não-estacionária, também pode usar alguma das seguintes técnicas:
- Criar uma nova série com os dados diferenciados: Z(t) = Y(t) – Y(t-1). Pode-se diferenciar os dados mais de uma vez, mas geralmente uma diferenciação é suficiente.
- Criar uma nova série aplicando o logaritmo ou raiz quadrada para estabilizar a variância (quadrado do desvio-padrão, relacionado a sua dispersão). Um exemplo é a transformação de Box-Cox (veja mais no respectivo item do post sobre Estatística). Para dados negativos, pode-se adicionar uma constante adequada para tornar todos os dados positivos antes de aplicar a transformação, que deverá ser subtraída do modelo para obter os valores ajustados e previsões para pontos futuros.
- Retirar tendência (se houver) ajustando algum tipo de curva aos dados (por exemplo, uma reta representando a tendência de longo prazo) e depois então modelar os resíduos daquele ajuste (falar o q são resíduos e gráficos que permitem analisá-lo). Os resíduos são a diferença entre o valor da série temporal utilizada e o valor modelado para o mesmo instante (no mesmo exemplo, o modelo de uma linha reta, para excluir a tendência linear de aumento/queda). A função decompose() apresenta um gráfico dos resíduos (parte aleatória, com a parte sazonal também retirada), que deve revelar que os erros são normais e independentes, com média zero e variância constante.
Modelagem
Um modelo é a forma matemática de se explicar um fenômeno. Quando o resultado do sistema é pré-determinado em função dos dados de entrada, esse sistema é chamado de determinístico; se o resultado do sistema não depende somente dos dados de entrada, mas também de outros fatores (normalmente aleatórios), é um sistema estocástico, e isso requer um modelo probabilístico.
Uma classe de modelos probabilísticos utilizados é a Suavização Exponencial. Enquanto na Média Móvel Simples as observações passadas são ponderadas igualmente, a Suavização Exponencial atribui pesos decrescentes exponencialmente quando a observação fica mais velha. Conforme o método, podem ser incluídas a tendência e a sazonalidade. Veja mais no post sobre Suavização Exponencial.
O modelo autoregressivo (AR) é uma regressão linear dos valores atuais da série contra um ou mais valores anteriores/posteriores da série. A ordem do modelo AR (número de regressões) é dada por um valor representado pela letra p. Já o modelo de média móvel (MA) está relacionado com erros passados, cujos termos são multiplicados por um coeficiente. A ordem do modelo MA é dada por um valor representado pela letra q.
Ambos os termos AR e MA podem ser usados no mesmo modelo, formando o chamado modelo ARMA. Se existe a necessidade de uma diferenciação, então essa série temporal é uma integral do modelo, surgindo assim o modelo ARIMA. Se a série tiver um padrão sazonal forte e consistente, você deve usar uma ordem de diferenciação sazonal (caso contrário, o modelo pressupõe que o padrão sazonal desaparecerá ao longo do tempo), gerando o modelo SARIMA (sazonal autoregressivo integrado de médias móveis). O modelo (S)ARIMAX incorpora um componente linear em função das observações das covariáveis. Mais informações nos posts sobre Modelo ARIMA e sobre Regressão Múltipla.
Autocorrelação e modelos
Depois de uma série temporal ser “estacionarizada”, o passo seguinte é determinar se os termos autorregressivos ou de médias móveis são necessários para corrigir qualquer autocorrelação que permaneça na série, assim como estimar suas respectivas ordens. Autocorrelação é a correlação entre os valores da série em um determinado período de tempo e os valores da mesma série em um outro momento. Essa ferramenta permite encontrar padrões de repetição. Mais informações sobre correlações estão disponíveis no link.
As função de autocorrelação (FAC, ou ACF em inglês) e da função autocorrelação parcial (FACP, ou PACF) da série contém os valores de autocorrelação em função do intervalo de tempo (lag) em que foi calculado. As FACP têm como objetivo filtrar correlações de outros lags e manter apenas a correlação pura entre duas observações. Os gráficos permitem identificar o número de termos autorregressivos e/ou de médias móveis que são necessários.
Veja algumas características especiais que podem ser útil no procedimento de identificação do modelo aos dados observados (caso não decaia conforme os lags aumentam, a série não é estacionária e precisa ser diferenciada antes de gerar os gráficos novamente):
- Aleatório – tudo zero ou próximo de zero (dentro dos limites do intervalo de confiança).
- AR(p) – decai de acordo com exponenciais e/ou senoides amortecidas, infinitas em extensão, ou alternando positivo e negativo, decaindo a zero; a autocorrelação parcial de um processo AR(p) é zero (considerando o intervalo de confiança) no lag p+1 e superior; um pico no lag 1 (por exemplo) indica uma forte correlação entre cada valor de série e o valor anterior (p=1), sendo que o lag 0 é sempre 1.
- MA(q) – apresenta um corte após o lag q(finita); se exibir um corte nítido e/ou a autocorrelação lag-1 negativa (ou seja, se a série aparecer ligeiramente “superdiferenciada”), então considere adicionar um termo MA ao modelo; o atraso para além do qual a ACF corta é o número indicado de termos MA.
- ARMA(p,q) – decai de acordo com exponenciais e/ou senoides amortecidas após o lag q-p, sendo infinita em extensão; se as estimativas de parâmetros no modelo original exigirem mais de 10 iterações para convergir, experimente um modelo com um termo de AR menos e um termo de MA menos (é possível que um termo de AR e um termo de MA cancelem os efeitos uns dos outros).
- ARIMA(p,d,q) – queda lenta nos primeiros lags da série, indicando que a série deve ser diferenciada; se a série tiver autocorrelações positivas para um alto número de atrasos (10 ou mais), então provavelmente precisa de uma ordem maior de diferenciação (após realizar a diferença, refazer o gráfico para reanalisá-lo); se a autocorrelação lag-1 é zero ou negativa, ou as autocorrelações são pequenas e sem padrão, a série não precisa de uma ordem maior de diferenciação (é estacionária, d=0); se d=1, possui tendência; se d=2, pressupõe uma tendência variável no tempo.
- SARIMA(p,d,q)(P,D,Q)[s] – valores altos em intervalos fixos; se a autocorrelação da série for positiva no intervalo s (onde s é o número de períodos em uma estação), considere adicionar um termo SAR ao modelo, e se for negativa, considere adicionar um termo SMA ao modelo; evitar o uso de mais de um ou dois parâmetros sazonais (SAR + SMA) no mesmo modelo, pois isso provavelmente levará à sobreposição de dados e/ou problemas de estimação.

Critérios baseados em informações de anos recentes, tais como FPE (Final Prediction Error) e AIC (Aikake Information Criterion), podem ser usados para ajudar a escolher o melhor modelo. Quanto menor o valor de AIC, melhor o ajuste. A função auto.arima() calcula os modelos e escolhe o de menor AIC (ou outro critério que escolher) – veja mais no post sobre Modelo ARIMA. Após algumas combinações dos parâmteros dos modelos, o com menor AIC é o modelo ARIMA(2,1,1)(1,1,1)[12], que também foi a escolha da função auto.arima().
Obs.: em alguns cálculos (principalmente com P=0 e Q=0), apareceu o erro “non-stationary seasonal AR part from CSS”. Isso acontece porque, ao usar CSS (soma condicional de quadrados), é possível que os coeficientes autoregressivos sejam não-estacionários. Para evitar esse problema, use a opção “method = c(‘ML’)” dentro da função “Arima()” (fonte: StackOverflow). Se for o caso (que não é o desse exemplo), pode ser também inserido o parâmetro “lambda = lambda” para receber o resultado “lambda = BoxCox.lambda(y)”.
Outra forma de avaliar o modelo é realizando a análise dos resíduos. A função tsdiag() plota os resíduos (geralmente padronizados), a função de autocorrelação dos resíduos e os p-valores de um teste de Ljung-Box para todos os atrasos até um determinado ponto (por padrão, 10 lags). O modelo deve apresentar os resíduos estacionários, com média zero e variância constante; se o gráfico dos resíduos mostra uma tendência sistemática positiva ou negativa, isso significa que outro modelo deve ser escolhido.

Com relação ao ACF, uma autocorrelação positiva é identificada por um agrupamento de resíduos com o mesmo sinal; a negativa é identificada por rápidas mudanças nos sinais de resíduos consecutivos. O ideal é todos os lags (exceto 0, que sempre vai ser igual a 1) tenham valores dentro do intervalo de confiança, ou seja próximos de zero, e sem tendências.
No teste de Ljung-Box (uma generalização do teste de Box-Pierce), a hipótese nula afirma que as autocorrelações até lag k são iguais a zero (ou seja, os valores dos dados são aleatórios e independentes até um certo número de lags). Se os valores tiverem uma dependência com seus antecessores (autocorrelação), isso pode reduzir a precisão de um modelo preditivo baseado no tempo e levar a uma interpretação incorreta dos dados.
Projeções
Modelos de séries temporais lineares, como ARIMA e modelos de suavização exponencial, preveem um futuro mais distante fazendo uma série de previsões de um período de antecedência e conectando-os para valores futuros desconhecidos. Por exemplo, uma previsão de 2 prazos é calculada tratando a previsão de 1 período anterior como se fosse de valores observados e depois aplicando a mesma equação de previsão. Esse procedimento pode ser repetido várias vezes, a fim de prever o futuro até quando quiser, mas cada vez com um intervalo de confiança maior.
Segue o gráfico para uma previsão de 12 meses usando o modelo escolhido conforme análise feita nesse post:
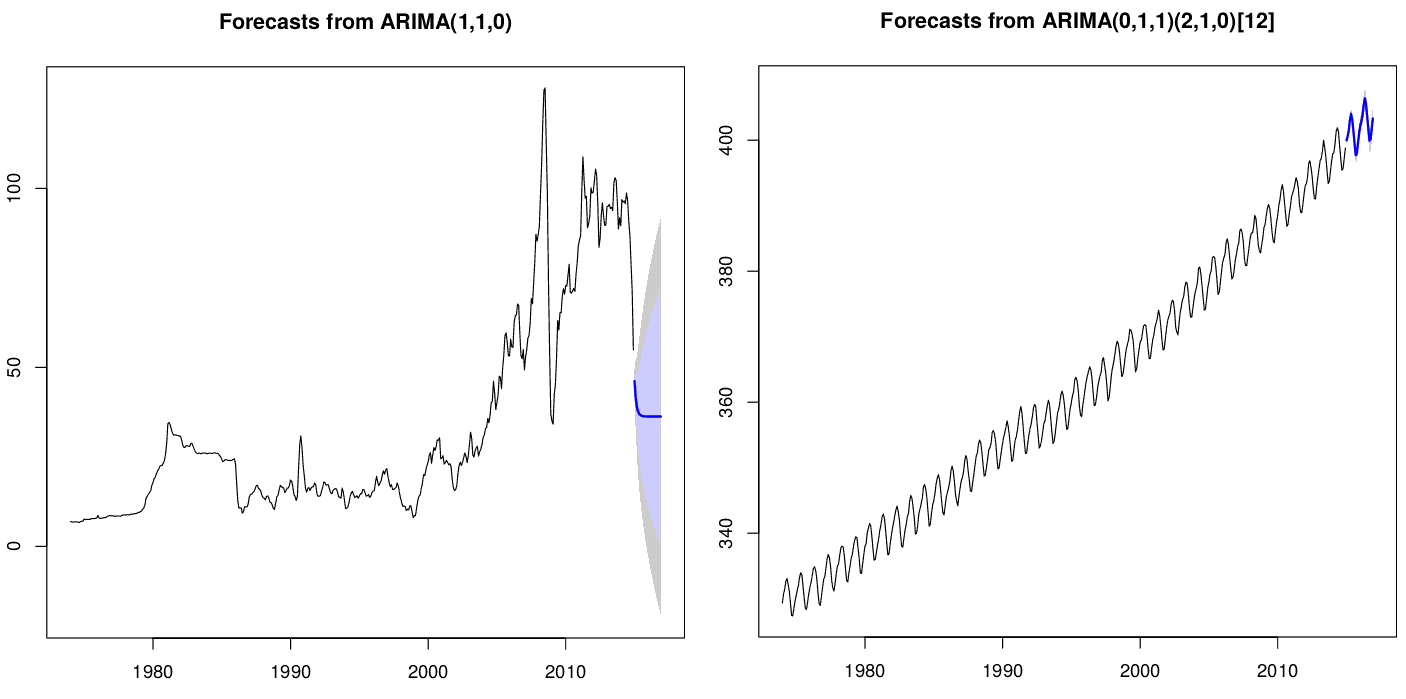
As sombras ao redor dos valores médios previstos são os intervalos de confiança: faixas de valores estimados onde a média tem uma dada probabilidade de ocorrer. Por padrão, os intervalos são de 80% e de 95% – existe 80%/95% de probabilidade que seu intervalo contenha o valor correto.
Variáveis explicativas (covariáveis)
Para gerar previsões de longo prazo ou mesmo previsões mais assertivas, seria bom aproveitar outras fontes de informação durante o processo de seleção do modelo e otimizar as estimativas de parâmetros para a previsão de vários períodos. Essa informação vem de variáveis independentes, também chamadas variáveis explicativas, exógenas, preditores, regressores, covariáveis ou mesmo variáveis de controle.
Primeiramente, os dados das duas séries devem ser tratados para retirar tendências, sazonalidades e autocorrelação (ou correlação serial). A função decompose, utilizada anteriormente, já calculou essa série para cada uma das duas séries temporais utilizadas como exemplo, e foram guardadas em uma data frame.
Para investigar a relação entre as séries temporais para saber se existe uma correlação entre suas variáveis, deve-se observar que nem sempre ocorre no mesmo ponto do tempo: muitas vezes um fenômeno antecede outro. Por isso, a correlação entre as séries não deve ser feita apenas pelo coeficiente de correlação usual (Pearson), devendo ser utilizada a função de correlação cruzada (CCF, em inglês).
O coeficiente de correlação é apresentado no eixo y de um gráfico em função do lag (eixo x), chamado de correlograma, e pode ser visto na imagem a seguir entre as variáveis dependente (concentração de gás carbônico) e independente (preço do barril de petróleo). A série que aparece primeiro na função ccf(y,x) é a da variável dependente (“resultado”), e a segunda é a da variável independente (“causa”). Lembrando que “lag” é o número de períodos de tempo que separam as duas séries temporais.
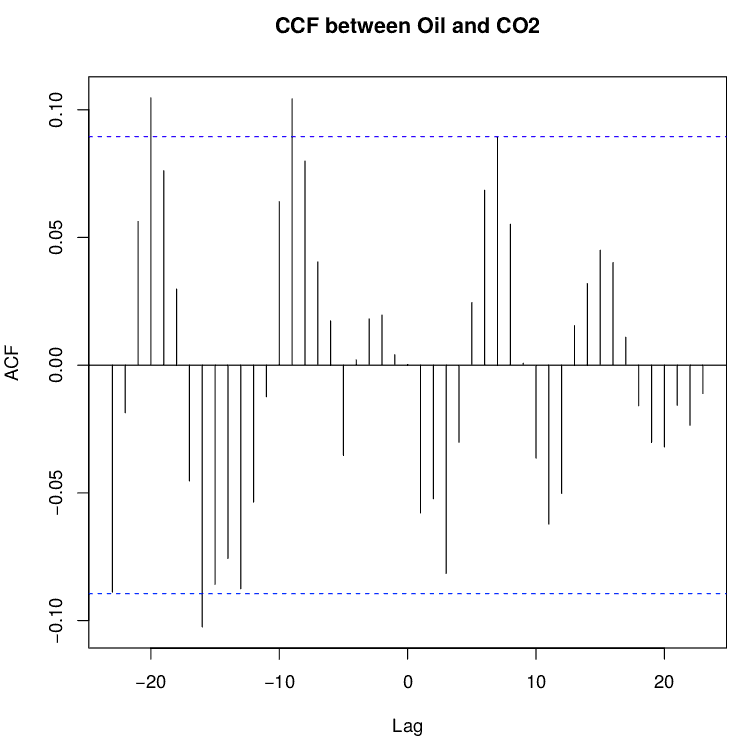
Os valores de correlação devem ter pico em lag igual a zero para não existir defasagem. Uma correlação cruzada com o desfasagem zero deve dar os mesmos resultados de uma correlação de Pearson normal, desde que sejam desconsiderados os campos NA que aparecem na série “decompose$random”.
Caso existam valores que ultrapassem o intervalo de confiança (linhas tracejadas), o lag escolhido será o com maior valor no eixo das ordenadas. Caso aplique a função lag(serie,n_lags) no lugar da série dentro da função ccf, todo o gráfico será deslocado em n_lags para a esquerda; usando n_lags negativo, o gráfico translada para a direita. A palavra “lag” significa “atraso”, então o sinal de negativo implica em um “avanço” da série (lead) – mais informações na documentação do R sobre a função lag.
O modelo Auto-Regressivo Integrado de Médias Móveis com entradas Exógenas (ARIMAX) acrescenta um termo à equação de previsão da variável y para cada tempo t, multiplicado por um coeficiente. Outra abordagem dessa questão é usar modelos de regressão com erros ARMA/ARIMA (ou seja, relacionados à regressão). A função arimax() do pacote TSA ajusta o modelo da função de transferência (mas não o modelo ARIMAX). A função arima() do R (Arima() e auto.arima() do pacote forecast) ajusta uma regressão com erros ARIMA, usando-se o argumento “xreg”. Mais detalhes no capítulo 9 Dynamic regression models disponível no link.
O lag de maior correlação, obtido pelo CCF, deve ser usado no cálculo do modelo. Também podem ser calculados diferentes modelos considerando diferentes valores de lag como regressores, ou mesmo mais de uma série de lags como regressores para um mesmo modelo, e escolher o de menor AICc. Um teste de Ljung-Box pode apresentar se os resíduos estão aleatórios (p-valor baixo).
O modelo escolhido pode ser usado para gerar uma previsão da série original. Para fazer uma projeção usando um modelo de regressão com erros ARIMA, é preciso prever as séries temporais usadas como regressores (previsões essas chamadas de preditores) e a parte ARIMA do modelo, e então combinar os resultados. Quando os preditores são conhecidos no futuro (por exemplo, variáveis relacionadas ao calendário ou saída de modelos numéricos de previsão de tempo), é só inclui-los na função. Mas quando os preditores são desconhecidos, devemos modelá-los separadamente ou usar valores futuros assumidos para cada preditor.
Avaliar projeções
Caso possua dados observados para o mesmo período de uma parte das previsões realizadas, pode-se fazer uso da tabela de contingência e taxas de acerto/falso alarme, etc (para fenômenos discretos) ou cálculo de erros (para variáveis contínuas). Suas definições podem ser vistas no post Métricas para comparar previsões.
Nesse exemplo, é analisado se a inclusão de uma variável regressora melhorou ou piorou a previsão da concentração de gás carbônico através das seguintes métricas:
- ME – Mean Error / Erro médio
- RMSE – Root Mean Squared Error / Raiz do erro quadrado/quadrático médio
- MAE – Mean Absolute Error / Erro médio absoluto
- MPE – Mean Percentage Error / Erro médio percentual
- MAPE – Mean Absolute Percentage Error / Média percentual absoluta do erro
- ACF1 – Autocorrelation of errors at lag 1 / Autocorrelação dos erros com 1 defasagem
- Theil’s U – U Statistic (veja mais no link)
A saída completa dos testes para as duas séries temporais do exemplo podem ser vistas no GitHub (arquivo output_tests.txt). Os valores das métricas para o caso “sem regressor” são menores, portanto a introdução de um regressor tende a piorar a previsão. Pode-se abortar o uso dessa variável explicativa ou melhorar sua previsão.
Fontes
- P. A. Morettin, C. M. C. Toloi, Análise de Séries Temporais, 2ª ed., São Paulo: Edgard Blücher, 2006 – livro base da disciplina MAE0325 – Séries Temporais do IME-USP
- Prof. Luiz Bertolo – Introdução à Análise de Séries Temporais
- Summary of rules for identifying ARIMA models
- ARIMA: Como evitar a mentalidade de rebanho ao analisar os dados de séries temporais
- O que é a estatística Ljung-Box q (LBQ)?
- Limpeza prévia dos dados para a função de correlação cruzada
- Applied Time Series Analysis – Moving Average Models (MA models)
- Rob J Hyndman – The ARIMAX model muddle
- Rob J Hyndman – Evaluating forecast accuracy
- TechnoFob – How To Find The Lag That Results In Maximum Cross-Correlation
- Forecasting: Principles and Practice – Lagged predictors
- ARIMAX Model Exercises (answers)


2 comments