Uma série temporal pode ser genericamente decomposta em Tendência, Ciclo, Sazonalidade e Aleatório – veja mais no post sobre Análise de Séries temporais. Basicamente, séries temporais que possuem tendência e/ou sazonalidade não são estacionárias e é necessário o uso de técnicas adequadas a tal situação. Existem testes não-paramétricos para identificar a existência de cada componente, mas justamente por sua alta correlação que devem ser usados com muita atenção.
Tendências
Alguns dos métodos mais utilizados para estimar a tendência consistem em ajustar uma função do tempo (como um polinômio ou uma exponencial), suavizar os valores da série ao redor de um ponto (para estimar a tendência naquela região) e/ou suavizar os valores da série através de sucessivos ajustes.
Após estimar a tendência, pode-se removê-la da série ponto a ponto para obter uma série temporal livre de tendência. Outro procedimento é normalmente utilizado para remover tendências é tomar sucessivas diferenças da série original até encontrar uma série estacionária.
O Teste de Wald-Wolfowitz (ou “runs test”) permite verificar se existe tendência em uma série temporal independente e identicamente distribuída.
Sua estatística é calculada com base na mediana da amostra, retornando um número de grupos com símbolos iguais adjacentes (ou “runs”). Por exemplo, considere uma “run” como um segmento não vazio máximo da sequência que consiste em elementos iguais adjacentes – por exemplo, a sequência de 22 elementos de comprimento “++++−−−+++−−++++++−−−−” consiste em 6 “runs”, 3 dos quais consistem em “+” e os outros de “-“. Considerando-se que cada elemento na sequência é extraído independentemente da mesma distribuição, o número de “runs” em uma sequência de N elementos é uma variável aleatória cuja distribuição condicional dada a observação de N + valores positivos e N- negativos é aproximadamente normal.
Sendo assim, considere as seguintes hipóteses:
- H0 (hipótese nula): “Não Existe tendência”
- H1: “Existe tendência”
Se o número de runs é significativamente maior ou menor do que o esperado, a hipótese de independência estatística dos elementos pode ser rejeitada.
Em um exemplo para 22 observações contínuas e mediana de 60054, resultou-se em um valor para o “runs” igual a 4 grupos distintos com símbolos iguais e p-valor de 0,00047326. Como o número de runs é significativamente menor do que o esperado (pois o p-valor é abaixo de 5%), rejeita-se a hipótese nula de que não existe tendência, ou seja, é muito provável haver tendência.
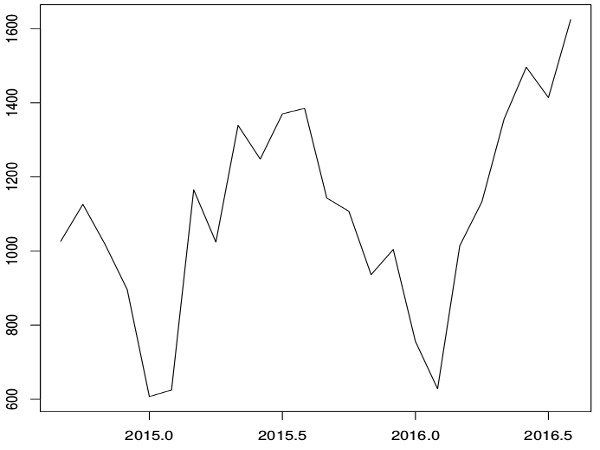
Nesse outro exemplo (série temporal A) para n = 24 dados, obteve-se valor de “runs” igual a 8 e p-value igual a 0.03688. Nesse caso, também é muito provável haver tendência.
O Teste de Cox-Stuart agrupa as observações em pares e associa os sinais de “+” ou de “-” conforme o resultado da comparação entre os elementos do par. O resultado da estatística apresenta o número de pares com sinal “+”.
Por exemplo, considerando a mesma série do primeiro exemplo, obtém-se uma estatística igual a 11 e um p-valor de 0,000488281. Assim, rejeita-se a hipótese nula e conclui-se que há tendência na série. O mesmo vale para o exemplo A (estatística = 9 e p-valor = 0.146).
O Teste de Mann-Kendall trabalha com a hipótese de que as observações da série possuem tendência monotônica no tempo (ou seja, há tendência), enquanto que a hipótese nula é que as observações são independentes e identicamente distribuídas.
Voltando aos dois exemplos, o primeiro possui o valor da estatítica igual a 0,77489 e p-valor igual a 0,000000477. Assim, rejeita-se a hipótese nula e conclui-se que há tendência na série. O mesmo vale para o exemplo A (estatística = 1.8851 e p-valor = 0.05941).
Para os três testes, existem funções em R no pacote randtests que realizam os cálculos das estatísticas:
# Teste de Wald-Wolfowitz runs.test(dados.ts) # Teste de Cox-Stuart cox.stuart.test(dados.ts) # Teste de Mann-Kendall rank.test(dados.ts)
Todas as funções recebem o parâmetro “alternative” para definir a hipótese alternativa. Usando “right.sided”, a hipótese nula de aleatoriedade é testada contra uma tendência crescente; para “left.sided”, a hipótese nula de aleatoriedade é testada contra uma tendência decrescente; e para “two.sided”, é testada contra uma tendência crescente ou decrescente.
Sazonalidade (ou periodicidade)
Uma série temporal é sazonal (periódica) quando os fenômenos se repetem a cada período idêntico de tempo – por exemplo, fenômenos que ocorrem diariamente em uma certa hora, todos os dias, ou em um certo mês em todos os anos. A sazonalidade determinística pressupõe um padrão sazonal regular e estável no tempo, o que permite prever o comportamento sazonal perfeitamente a partir de dados anteriores – modelos de regressão como o MMQ são muito aplicados nesse tipo de série. Já a sazonalidade estocástica é quando a componente sazonal da série varia com o tempo.
Também é possível utilizar métodos paramétricos e não paramétricos para determinar sazonalidade determinísticas, sendo necessário eliminar antes a tendência da série se ela existir. Considera-se que não existe sazonalidade determinística na série temporal se a hipótese nula de que todos os coeficientes dos termos sazonais são nulos não for rejeitada.
O Teste de Kruskal-Wallis supõe uma amostra de uma população, subdividida em ‘k >= 4’ conjuntos de amostras com tamanho ‘n’ não necessariamente iguais entre si – por exemplo, para uma série anual com observações mensais, n = 12 e k é o número de anos. Ele também é usado para testar se um conjunto de amostras provêm da mesma distribuição – testa-se a hipótese nula de que todas as populações possuem funções de distribuição iguais contra a hipótese alternativa de que ao menos duas das populações possuem funções de distribuição diferentes.
Já o Teste de Friedman divide a série em blocos de períodos e calcula o posto de cada observação em cada bloco – por exemplo, uma série com dados mensais durante 20 anos para testar a sazonalidade em cada mês durante os 20 anos, têm-se um período de 12 meses e 20 blocos de períodos.
Em ambos os testes, define-se a expressão da estatística H para o teste e pode ser calculado seu valor numérico. A distribuição de H pode ser aproximada por uma distribuição qui-quadrado com ‘k-1’ graus de liberdade.
No R, o pacote PMCMR permite realizar alguns testes de sazonalidade, como os descritos acima. Note que os dados devem ser separados em grupos (um para cada ano com os dados mensais, por exemplo) para o cálculo da estatística:
# Teste de Kruskal-Wallis month = format(as.Date(var_y$date), "%m") # criar vetor com meses var_y = cbind(var_y,month) print(kruskal.test(var_y$value ~ var_y$month, var_y)) # Teste de Friedman year = format(as.Date(var_y$date), "%Y") # criar vetor com anos var_y = cbind(var_y,year) print(friedman.test(var_y$value,var_y$year,var_y$month))
O p-valor é aproximado pela probabilidade na distribuição qui-quadrado bicaudal para o valor de H. Caso essa probabilidade dê aproximadamente zero, rejeita-se a hipótese nula de que não existe sazonalidade determinística, ou seja, é muito provável que exista sazonalidade.
Decomposição STL
STL é um acrônimo para “Decomposição sazonal e de tendência usando Loess”, sendo que “Loess” é um método para estimar relações não-lineares. As componentes de sazonalidade e de tendência são evidenciadas em gráficos, permitindo melhor visualização desses fenômenos na série temporal.
No R, o pacote forecast dispões de funções para realizar essa decomposição e plotar em gráficos:
- stl () – permite uma decomposição de qualquer frequência.
- stlm () – toma uma série temporal, aplica a decomposição STL, modela os dados ajustados sazonalmente usando o modelo especificado (neste caso ARIMA ou ETS).
- stlf () – combina as funções stlm () e forecast (), seleciona automaticamente o modelo que é considerado a melhor escolha.
Não funcionam se a série não é periódica ou tem menos de dois períodos. A função forecast.stl realiza uma previsão usando objetos stl.
Fontes

3 comments