Existem diferentes formas de quantificar a associação entre dois grupos (dados observados e modelados, por exemplo) através de parâmetros. A correlação é uma das formas para quantificar o grau de associação/dependência entre duas amostras/variáveis, indicando a força e a direção do relacionamento linear. Uma correlação negativa indica que as duas variáveis movem-se em direções opostas – por exemplo, a temperatura está aumentando para os dados observados enquanto que para a previsão os valores estão diminuindo.
O coeficiente de correlação (geralmente chamado de R, r ou ρ) mais conhecido é o coeficiente de correlação de Pearson. É calculado pela razão entre a covariância de duas variáveis e o produto de seus desvios padrão. A covariância entre duas variáveis pode ser obtida de dados de variância, que é uma medida da sua dispersão estatística, indicando “o quão longe” em geral os seus valores se encontram do valor esperado. Outra forma de calculá-lo é tirando-se a raiz quadrada de r² (explicação mais a frente) ou através da seguinte fórmula:
\(\rho=\frac{\sum\limits_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum\limits_{i=1}^{n}(x_i-\overline{x})^2}\cdot\sqrt{\sum\limits_{i=1}^{n}(y_i-\overline{y})^2}}=\frac{cov(X,Y)}{\sqrt{var(X)\cdot var(Y)}}\)Seu valor varia entre -1 e 1 (indicam correlação total); quando igual a zero, pode não haver correlação ou não existir uma relação não linear entre duas variáveis. Leia também o artigo “Desvendando os Mistérios do Coeficiente de Correlação de Pearson“. Existem também os coeficientes de Kendall e de Spearman para dados que não sigam uma distribuição normal.
O coeficiente de determinação (também chamado de R², r², R-squared ou correlação quadrática) é indicador usado para medir a qualidade de um ajuste em relação aos valores observados. Varia entre 0 e 1 e mostra o quanto que x explica y, podendo ser representado percentualmente; quanto maior o R², os pontos estão menos dispersos ao redor do ajuste e mais o modelo se ajusta à amostra. Pode ser calculado como o quadrado do coeficiente de correlação ou também diretamente através da seguinte fórmula:
\(R^2=1-\frac{SQE}{SQT}=1-\frac{\sum\limits_{i=1}^{n}(y_i-\overline{y})^2}{\sum\limits_{i=1}^{n}(y_i^{est}-\overline{y})^2}\)Onde SQE é a Soma dos Quadrados Explicada (indica a diferença entre a média das observações e o valor estimado para cada observação; quanto menor for a diferença, maior poder explicativo detém o modelo) e SQT é a Soma Total dos Quadrados (a soma dos quadrados das diferenças entre a média e cada valor observado), que também é a soma entre a SQE e a SQR (Soma dos Quadrados dos Resíduos, que calcula a parte que não é explicada pelo modelo).
Note que a inclusão de muitas variáveis aumenta o valor de R², mesmo que tenham muito pouco poder explicativo sobre a variável dependente. Isso prejudica o princípio da parcimônia, cuja recomendação é a de que se escolha a teoria explicativa que implique o menor número de premissas assumidas e o menor número de entidades. Para combater esta tendência de incluir um número exagerado de variáveis explicativas, existe o R² ajustado, que penaliza a inclusão de regressores pouco explicativos, definido por:
\(\overline{R^2}=1-\frac{n-1}{n-(k+1)}(1-R^2)\)Onde k é o número de variáveis explicativas.
Quando você eleva ao quadrado o valor do coeficiente de correlação (R), obtém o coeficiente de determinação (R²). As diferença entre Coeficiente de Correlação (R) e Coeficiente de Determinação (R²) também são vistas nesse vídeo:
O coeficiente de correlação múltipla é definido por meio de uma extensão do coeficiente de correlação entre duas variáveis. Quando usada uma equação de regressão linear, é chamado coeficiente de correlação múltipla linear. Considerando-se uma variável dependente z e duas independentes (x e y), pode-se escrever a definição desse coeficiente em função dos coeficientes lineares entre as variáveis duas a duas:
\(R_{z,xy}=\sqrt{\frac{r^{2}_{xz}+r^{2}_{yz}-2r_{xz}r_{yz}r_{xy}}{1-r^{2}_{xy}}}\)Quanto mais próximo de 1, mais bem definida será a relação linear entre as variáveis, e quanto mais perto de 0, menos acentuada ela será.
O Qui-quadrado (χ²) mede o afastamento global dos dados observados em relação a uma “distribuição esperada” (uma regressão linear ajustada/calculada a partir dos dados observados), expresso por:
\(\chi^2=\sum\limits_{i=1}^{n}\frac{(o_i-e_i)^2}{e_i}\)Para calculá-lo, toma-se a diferença entre o valor observado e o esperado, eleva-se ao quadrado e divide-se pelo valor esperado, repetindo-se o procedimento para todos os valores e realizando um somatório geral. Quanto mais perto de zero, menos discrepantes estão os dados e o modelo. A amostragem deve ser aleatória, sem dados contendo viés (tendência).
Os casos acima funcionam para regressão linear. Para regressão não-linear (como no modelo ARIMA), utiliza-se o método da Máxima Verossimilhança (ou MLE, do inglês maximum-likelihood estimation) e critérios baseados nessa definição, como o Critério de Informação de Akaike (AIC) – maiores detalhes pódem ser vstos no post sobre o Modelo ARIMA.
Correlação cruzada
Pensando em processamento de sinais, a relação (ou correlação) cruzada é uma medida de similaridade entre dois sinais em função de um atraso aplicado a um deles, frequentemente usada para procurar um sinal de curta duração que esteja inserido em um sinal mais longo. Na relação entre duas séries temporais, uma delas pode estar relacionada com a outra por uma diferença de passo. Por exemplo: um excesso de chuvas podem causar o aumento de pontos com água parada e proliferanção de ovos e mosquitos, mas somente 1 ou 2 meses depois é que os casos de dengue aumentam.
A função de correlação cruzada da amostra (CCF, do inglês cross correlation function) é útil para identificar defasagens da variável – atrasos (lags) ou avanços (leads) -, que podem ser preditores úteis da série principal. A correlação é definida entre y(t) e x(t+h), onde h é um número inteiro:
- positivo (“x lags y”, a série x é adiantada com relação à y, cortando o último valor de y para as séries terminarem no mesmo instante);
- negativo (“x leads y”, a série y é adiantada com relação à x, cortando o último valor de x para as séries terminarem no mesmo instante).
A CCF é basicamente definida como o coeficiente de correlação de Pearson, mas agora conta com uma defasagem h (note que a CCF iguala-se à função de autocorrelação se X(t)=Y(t)):
\(\rho_{XY}(h)=\frac{cov(X_t,Y_{t+bh})}{\sqrt{var(X_t)\cdot var(Y_{t+h})}}\)Na função lag(vetor,k=numero_de_lags) do R, o vetor de variáveis recebe um NA no lugar do valor vacante para diferenças acima de 1 tempo, de modo a manter o tamanho do vetor. Para k < 0, a série "anda" para frente (aparecem NAs no começo da série e são cortados valores mais recentes); para valores positivos de k, a série "anda" para trás (aparecem NAs em instantes mais recentes e são cortados valores mais antigos).
Em alguns problemas, o objetivo pode ser identificar qual variável está à frente e qual está atrasada. No entanto, geralmente consideramos que examinaremos a(s) variávei(s) x como uma variável com avanço (lead) com relação à variável y, porque queremos usar valores de x para prever valores futuros de y. Ou seja, estaremos olhando o que está acontecendo nos valores positivos de h no gráfico do CCF.
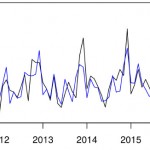
Para calcular e imprimir um gráfico das correlações cruzadas, use o seguinte comando no R: ccf(x,y,numero_de_lags_do_grafico). Será impresso um correlograma, que consiste em um gráfico tipo densidade, onde cada ponto do eixo x corresponde a um lag e o seu valor no eixo y é o coeficiente de correlação naquele lag. Para ver melhor os valores, atribua um objeto para receber a função e a imprima.

Na imagem de exemplo, note que as correlações na região com maior magnitude são negativas, indicando que um valor ACIMA da média de x é susceptível de levar a um valor ABAIXO da média de y cerca de 12 meses depois (considera-se 12 pois esse é o lag com valor com maior valor no eixo das ordenadas, que é 0.293). As séries sazonais são caracterizadas por apresentarem correlação alta em “lags sazonais” (múltiplos do período “de ano em ano”).
Observação: os dados brutos não devem ser utilizados diretamente, porque as estruturas presentes em ambas as séries (como tendências, sazonalidades e correlação serial) podem levar ao diagnóstico de correlações cruzadas espúrias entre as séries estudadas. Por exemplo, a presença de correlações cruzadas significativas em vários lags diferentes, resultado de uma correlação entre as estruturas seriais das duas séries, ocasionando uma falsa interpretação.
Autocorrelação
Quando ambas as funções de entrada em uma relação cruzada são a mesma função, a relação cruzada é conhecida por autocorrelação (ACF, do inglês autocorrelation function). Autocorrelação é simplesmente a correlação entre os valores da série em um determinado período de tempo e os valores da mesma série em um outro momento no tempo – ou seja, entre a série e ela mesma defasada.
A autocorrelação é uma ferramenta matemática para encontrar padrões de repetição, como a presença de um sinal periódico obscurecidos pelo ruído. Um diagrama de autocorrelações apresenta os valores de autocorrelação de uma amostra versus o intervalo de tempo em que foi calculado. Autocorrelações devem ser próximas de zero para aleatoriedade. A ocorrência de não estacionariedade é denotada pela lenta queda da ACF nos primeiros lags da série. Isto significa que a série deve ser diferenciada, e que um modelo ARIMA ou SARIMA deve ser aplicado.

As linhas tracejadas do correlograma acima mostram o intervalo de confiança, que indica onde é significativamente diferente de zero: quando praticamente todos os valores ACF estão dentro desses limites, a autocorrelação é igual a zero, indicando que a série é aleatória. Uma correlação positiva indica que grandes valores atuais correspondem aos valores grandes no lag especificado, e uma correlação negativa indica que grandes valores atuais correspondem aos valores pequenos no lag especificado.
O correlograma também é usado para analisar os resíduos de um modelo. Ao fazer uma projeção (forecast), o correlograma do resíduo desse modelo deve estar contido nos limites tracejados. Ou seja, os resíduos não podem ter autocorrelação. Caso contrário, sua projeção pode ser melhorada, pois alguma informação relevante no modelo está contida nos resíduos (análogo ao que foi comentado nos textos de Regressão Linear).
Já a autocorrelação parcial (FACP) é a correlação entre as observações em uma série temporal que não é contabilizada por todos os intervalos mais curtos entre essas observações. Tem como objetivo filtrar correlações e manter-se apenas a correlação pura entre duas observações. Esta medida corresponde a correlação de x(t) e x(t-k) removendo o efeito das observações x(t-1), x(t-2) … x(t-k+1). Por exemplo, em uma autocorrelação parcial para um lag de 6 é apenas a correlação que não é contabilizada por lags de 1 a 5.

Tanto a autocorrelação quanto a autocorrelação parcial indicam quais valores de série anteriores são mais úteis para prever valores futuros. Com esse conhecimento, é possível determinar a ordem dos processos no modelo ARIMA. Por exemplo, um pico no lag 1 em um gráfico FAC indica uma forte correlação entre cada valor de série e o valor anterior – AR(1); um pico no lag 2 indica uma forte correlação entre cada valor e o valor que ocorre dois pontos antes – AR(2) -, e assim por diante. É útil para identificar modelos AR puros, não sendo tão útil para identificar modelos MA e ARMA.
Os modelos citados são apropriados para descrever séries estacionárias, ou seja, que se desenvolvem no tempo ao redor de uma média constante. No entanto, várias séries econômicas e financeiras podem tornar-se estacionárias quando diferençadas. Se a série diferençada for estacionária, então a série original é uma integral da série diferençada. Veja mais no post sobre modelo ARIMA e modelo ARIMA no R clicando nos links.
Causalidade de Granger
O teste de causalidade proposto por Clive William John Granger visa superar as limitações do uso de simples correlações entre variáveis, determinando o sentido causal entre duas variáveis. Uma variável X causa outra variável Z no sentido de Granger se a observação de X no presente ou no passado ajuda a prever os valores futuros de Z para algum horizonte de tempo.
A popularidade dos modelos VAR (modelos autorregressivos vetoriais) deriva, em grande medida, da percepção de que tais modelos permitem analisar as inter-relações entre múltiplas variáveis a partir de um conjunto mínimo de restrições de identificação. O VAR pode ser identificado através de uma decomposição de Cholesky na qual a ordenação causal é definida em conformidade com os resultados de testes de causalidade de Granger, sob a hipótese implícita de que a ausência de causalidade (no sentido de Granger) de uma variável X para outra variável Z deve implicar a ausência de efeito contemporâneo de X sobre Z. Por outro lado, o fato de certa variável X não causar outra variável Z no sentido de Granger não é condição necessária nem suficiente para a ausência de efeito contemporâneo de X sobre Z.
Existem funções em R, como a causality, que implementam o teste – sua hipótese nula H0 é relativa à “Granger Não-Causa”.
Fontes
- Applied Time Series Analysis – Cross Correlation Functions and Lagged Regressions
- Estatsite – Séries temporais: correlograma
- Rpubs – Correlação, Autocorrelação e Autocorrelação Parcial
- IBM – Funções de Autocorrelação e de Autocorrelação Parcial
- Portal Action – Identificação de Modelos Arima
- Autocorrelação espacial e correlogramas no R

Excelente post. Parabéns pelo site!
Opa, obrigado pela visita e pelo comentário! Seu site é muito bom também. Tenho muito interesse em estatística, particularmente em previsão de séries temporais. Vou ler tudo por lá! rsrs Descobri o https://estatsite.com pelo Google, não tinha me ligado que você também era redator no Deviante.
Que bom que gostou! Estou um pouco em dívida com séries temporais rs, mas aos poucos vou postando mais.
Sou redator do deviante sim! Bacana que você conhece.
Boa essa troca de ideias.
Abraços