Lei de Benford

Suponha que você precise verificar se o balanço contábil de uma empresa está fraudado ou não. A intuição nos diz que, se a pessoa que lançou valores aleatórios, a probabilidade do primeiro dígito de cada valor ser 1 é a mesma de ser 2, e assim por diante (11,1% para cada dígito). No entanto, os balanços reais e sem fraudes não possuem essa distribuição. Na verdade, a probabilidade do primeiro dígito ser 1 é de mais ou menos 30%, de ser 2 é aproximadamente 17%, e assim por diante conforme a tabela a seguir:

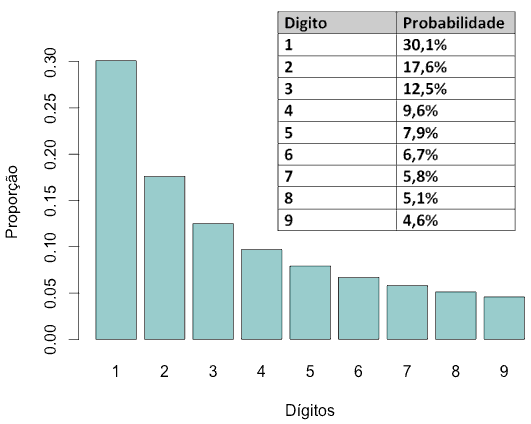
A lei de Benford, também chamada de lei do primeiro dígito, foi definida empiricamente e refere-se à frequência da distribuição de dígitos em vários casos reais. Seu nome é uma homenagem ao físico Frank Benford, que a declarou em 1938 (seu artigo, The Law of Anomalous Numbers, pode ser consultado nesse link), embora tenha sido anteriormente afirmada por Simon Newcomb em 1881. O resultado investigado por Benford não define apenas uma distribuição para os primeiros dígitos, mas uma distribuição para todos os dígitos significativos de um número.

A comparação da distribuição dos dígitos de uma amostra qualquer com a distribuição de valores segundo a Lei de Benford é uma ferramenta muito utilizada na auditoria contábil e em vários outros campos da economia e das ciências sociais. Espera-se que uma distribuição obedeça a Lei de Benford quando: a média é maior do que a mediana e a inclinação é positiva; os números sejam resultantes da combinação matemática de números (quantidade × preço, por exemplo). Boa parte das sequências numéricas, valores influenciados pelo pensamento humano (preços R$1,99, por exemplo), contas com valores específicos fixos e casos semelhantes não seguem essa lei.

Uma forma de se quantificar a comparação do quanto a distribuição de valores da amostra está próxima à Lei de Benford é através da estatística de chi-quadrado. Quanto maior o valor de chi-quadrado, maior a discrepância entre a lei e os dados, e também maior a chance de ter havido fraude.

Exemplo

Os dados utilizados para esse exemplo foram retirados da página do Tribunal Superior Eleitoral (TSE) – SPCE WEB. Referem-se ao financiamento de campanhas das eleições de 2014. Um arquivo CSV pode ser baixado e lido pelo R, desde que apagada a última linha e os caracteres “R$ ” serem removidos, além de converter tirar o ponto como separador de milhar e substituir a vírgula para ponto com separador decimal. Isso pode ser feito através do seguinte comando em bash, redirecionando a saída para o arquivo “receita_candidato.csv”:

cat receita.csv | awk -F';' '{print $7}' | sed 's/R\$\ //g' | sed 's/\.//g' | sed 's/,/./g' > receita_candidato.csv

Existe um pacote no R que facilita bastante a análise de comparação com a Lei de Benford, o benford.analysis. O autor dispõe algumas análises em seu blog, o Análise real – tag Lei de Benford. Para instalar o pacote (em uma “library” diferente da padrão), use o seguinte comando:

> install.packages("benford.analysis", dependencies=TRUE, lib="~/Rpacks")

O seguinte script em R carrega a biblioteca instalada e a série de dados, além de fazer os gráficos para serem analisados (i é o número do candidato analisado):

#!/usr/bin/Rscript
# Script para aplicar a Lei de Benford em uma série de dados

# Definindo bibliotecas conforme endereço (suprimindo mensagens iniciais)
end_libs="~/Rpacks"
suppressPackageStartupMessages(require(benford.analysis,lib=end_libs))

# Carregamento de dados
i = 0
filename = paste('receita_',i,'.csv', sep = '')
dados = read.csv(filename, header = TRUE, stringsAsFactors = FALSE)

# Analisar os dados contra a lei de Benford
bfd.cp = benford(dados$Valor)

# Imprimir resultados
print(bfd.cp)
cat('\n\n') # quebra de linha

# Analisar suspeitos
suspeitos = getSuspects(bfd.cp, dados)
print(suspeitos)

# Plotar gráficos
filename = paste('receita_',i,'.png', sep = '')
png(filename)
plot(bfd.cp)
dev.off()

A função “benford()” analisa os dois primeiros dígitos dos valores positivos como padrão. A impressão do objeto resultante exibe estatísticas importantes para a análise:

Benford object:
 
Data: dados$Valor 
Number of observations used = 487 
Number of obs. for second order = 284 
First digits analysed = 2

Mantissa: 

   Statistic Value
        Mean  0.46
         Var  0.09
 Ex.Kurtosis -1.27
    Skewness  0.21


The 5 largest deviations: 

  digits absolute.diff
1     15         70.35
2     50         19.81
3     10         12.84
4     13         11.67
5     11         10.40

Stats:

	Pearson's Chi-squared test

data:  dados$Valor
X-squared = 639.13, df = 89, p-value < 2.2e-16


	Mantissa Arc Test

data:  dados$Valor
L2 = 0.017652, df = 2, p-value = 0.0001847

Mean Absolute Deviation: 0.007708392
Distortion Factor: -7.515548

Remember: Real data will never conform perfectly to Benford's Law. You should not focus on p-values!

      Valor
  1:   1500
  2:   1500
  3:    150
  4: 500000
  5:  50000
 ---       
104:   1500
105:   1500
106:   1500
107:   1500
108:   1500

Além de dados gerais, são exibidas estatísticas da mantissa (parte do número em ponto flutuante que contém os dígitos significativos), os cinco maiores desvios, chi-quadrado e outras informações. Para seguir a Lei de Benford, as principais estatísticas da mantissa do log devem seguir os valores:

• média: 0.5
• variância: 1/12 (0.08333…)
• curtose: 1.2
• assimetria: 0

Quanto ao ranking dos maiores desvios, esses dados “suspeitos de fraude” podem ser analisados através da função getSuspects(). Sua saída é uma tabela com os dados dos dois grupos de dígitos com maior discrepância (pela diferença absoluta).

Quando o objeto resultante dessa função é plotado, são impressos gráficos dos dados em comparação com a Lei de Benford (em vermelho), conforme segue:

O primeiro gráfico contém a distribuição dos valores, o segundo mostra a contagem para a diferença dos dados ordenados e o terceiro contém soma dos valores das observações agrupadas por primeiros dígitos.

Análise

Através do primeiro gráfico apresentado, assim como o ranking dos maiores desvios, é possível observar uma grande discrepância nos valores que começam com “15” ou com “50” se comparados aos valores esperados conforme a lei de Benford. Com relação ao segundo gráfico, como os dados são discretos, este saltos decrescentes em 10, 20, 30… são naturais e não devem ser encarados como algo suspeito.

Esses valores discrepantes constituem uma amostra menor do que o total de dados, podendo ser encaminhados para uma análise mais detalhada. Uma explicação seria uma proposta de doação com um valor fixo de 1500 reais, e assim muitas pessoas teriam feito esse tipo de doação. Por outro lado, existe a possibilidade de terem sido inventadas doações ou valores diferentes dos realmente doados.

A apresentação a seguir fala um pouco mais sobre o que foi descrito até aqui:

Aplicações

Em 1993, no estado do Arizona, Wayne James Nelson foi acusado e considerado culpado por roubar o Estado quase US$ 2 milhões, desviando fundos para um vendedor falso. James foi pego por fraudar pagamentos com a intenção de fazê-los parecer aleatórios. Ele quis caprichar demais, não duplicando nenhum valor nos cheques, evitando números arredondados. Sem perceber, ao caprichar, o fraudado não percebeu que suas escolhas aparentemente aleatórias estavam longe de ser aleatórias.

Nos EUA, evidências de fraude e sonegação de imposto são legalmente admissíveis pela aplicação da “Lei de Benford” em casos criminais federais, estaduais e locais. As empresas de auditoria utilizam programas específicos, capazes de identificar alterações para que seus analistas possam investigar a fundo possíveis irregularidades. Quando há mais dígitos baixos do que o previsto na lei (principalmente 5, 6 e 7, e menos dígitos entre 1 e 5) é indício de fraude.

Em outubro de 2018, circularam vídeos na internet brasileira dizendo que as eleições de 2014 teriam tido uma alta probabilidade de terem sido fraudadas graças à Lei de Benford. No entanto, ela não é bem observada em conjuntos de dados com menos de 500 transações – que é o caso de todas as seções eleitorais. Michelle Brown, da Universidade de Georgetown, aplicou a tal lei nos dados de votos de uma assembleia nos EUA e descobriu que a Lei de Newcomb-Benford não é confiável para analisar eleições. Outro estudo, feito por professores da Universidade de Oregon e do Instituto de Tecnologia da Califórnia, nos EUA, confirmou que o conceito é inútil para cenários eleitorais. Veja mais no site e-farsas.

A Operação Serenata de Amor foi criada com foco na Cota para o Exercício da Atividade Parlamentar da Câmara dos Deputados como uma forma de detectar corrupção nesses gastos. Nela, são usadas desde regras simples de limites, análises matemáticas (como a Lei de Benford) e características dos próprios gastos (como local e hora em que foi realizado e comparação em categorias). Tudo isso usando dados públicos e uma inteligência artificial para selecionar as “melhores” denúncias e informar os cidadãos. Essas ferramentas mostram como a Lei de Benford pode ser somente uma de várias ferramentas na busca de fraudes em diferentes tipos de contabilidades.

Ouça sobre a Lei de Benford no episódio 154 do podcast Naruhodo e veja mais no blog da Jessica Temporal. Alguns exemplos da Lei de Benford aplicada a obras públicas podem ser vistos no site do TCU.