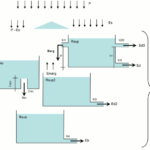
Esse post aborda alguns tópicos importantes de métodos numéricos com foco na modelagem atmosférica e sobre a parametrização de processos da atmosfera. Modelos numéricos de previsão de tempo necessitam que a atmosfera seja representada por uma malha computacional, que pode ser estruturada ou não. A discretização espacial também pode ser de diferentes formas: diferenças finitas, volume finito, espectral, lagrangiano. Cada modo com vantagens e desvantagens.
A malha estruturada, composta de retângulos 2D, tem como vantagens a facilidade em manipular os índices e armazenar informações, com uma conectividade limpa. Como desvantagem, tem menor eficiência para malhas localmente refinadas e apresenta dificuldade para envolver geometrias complexas, com restrições à ortogonalidade e razão de aspecto.
A malha não-estruturada, composta de diferentes formas geométricas 2D, tem como vantagens a robustez na representação de geometrias complexas e maior eficiência para malhas localmente refinadas. Como desvantagens, apresenta dificuldade em armazenar e manipular dados na computação, necessitando armazenar as informações de conectividade para cada célula.
O método das diferenças finitas resolve equações diferenciais baseando-se na aproximação de derivadas por diferenças finitas, com a fórmula de aproximação obtida da série de Taylor da função derivada. Como vantagem, são intuitivos e fáceis de implementar para problemas simples. Como desvantagem, eles rapidamente se tornam difíceis de manejar se precisar adicionar algum tipo de complexidade, como mover limites ou uma grade não estruturada, e não são bons para grande descontinuidade.
No método de volume finito, as equações governantes (na forma diferencial) são médias de volume, integradas em cada elemento de volume da grade. As integrais de volume do teorema de Gauss são convertidas em fluxos de concentração ou momentum sobre os limites da superfície do volume. As equações de transporte podem ser escritas em forma de fluxo, de modo que a taxa de variação de uma quantidade dentro de um volume de controle depende dos fluxos através do limite. Como vantagens, as leis de conservação também são satisfeitas na representação discreta, o que é essencial para lidar corretamente com a descontinuidade de um salto, como uma onda de choque. Apesar dos fluxos terem mais significado físico, como desvantagem as geometrias irregulares requerem muito mais esforço.
O método Espectral usa a decomposição de um sinal físico na soma de uma série de ondas simples de diferentes amplitudes. Ele usa funções de base “globais” ortogonais que são diferentes de zero em todo o domínio e funções de base “local” que são diferentes de zero apenas em pequenos subdomínios. Como vantagem, é um método muito preciso quando a solução é suave , devido a boas propriedades de erro de “convergência exponencial”, e com geometria simples (periódica, por exemplo), sendo mais leve computacionalmente nesses casos. Como desvantagem, não é bom para problemas descontínuos (nenhum resultado de “captura de choque” espectral 3D conhecido) e vinculam ao fenômeno de Gibbs.
O método Lagrangiano envolve seguir as partículas fluidas e determinar como as propriedades da partícula variam em função do tempo – descrição oposta à Euleriana. Um esquema semi-Lagrangiano, amplamente utilizado em modelos numéricos de previsão do tempo para a integração das equações que governam o movimento atmosférico, usa a estrutura Euleriana, mas as equações discretas vêm da perspectiva Lagrangiana. Ele requer dois cálculo importantes: o cálculo do ponto de partida e a interpolação do campos advectado do ponto de partida. Suas principais vantagens são suas boas propriedades de estabilidade e dispersão, que, quando combinadas com a discretização semi-implícita ou totalmente implícita dos termos não aditivos, geram modelos muito robustos, precisos e eficientes. Como desvantagem, existe a falta de conservação formal de quantidades, como a massa, devido à interpolação.
Uma discussão sobre a resolução numérica das equações usando o método de Runge-Kutta e os erros das soluções numéricas pode ser vista no post Erros de soluções numéricas e Runge-Kutta, com dois exemplos práticos.
Parametrização
Dentre as equações que descrevem os processos físicos que ocorrem na atmosfera, alguns de seus termos são dependentes dos momentos de 2ª ordem:
Na equação de momentum, depois dos termos de advecção média (à esquerda da igualdade), gravidade, Coriolis, gradiente de pressão e estresse viscoso (da esquerda para direita), estão os termos de transporte turbulento. Na equação do calor, depois dos termos de advecção média (à esquerda da igualdade), radiação e liberação de calor latente, estão os termos de transporte turbulento. Na equação de água total, depois dos termos de advecção média (à esquerda da igualdade) e precipitação, estão os termos de transporte turbulento.
Os termos de transporte turbulento são fluxos de momento de segunda ordem que podem ser parametrizados. A parametrização descreve processos que não podem ser resolvidos na malha (menores do que a célula de grade). Esses processos estão relacionados à absorção de energia solar na superfície, que é o motor para os movimentos atmosféricos, e às variações mais abruptas nas variáveis atmosféricas típicas das camadas mais próximas da superfície do planeta (condição de contorno inferior para os movimentos atmosféricos). Assim, os termos de transporte turbulentos foram divididos em superfície (sfc), camada limite (pbl) e convecção (conv), além de solo (gwd) na equação de momentum.
A equação do fluxo de massa é usada para lidar com o transporte turbulento convectivo de calor e massa:
\(\overline{-w’x’}=gM^c(x^c-\bar{x})\)
O fluxo de massa é o produto de uma velocidade vertical w de escala convectiva e uma fração de área, e que em esquemas de parametrização, geralmente só é possível determinar o fluxo de massa com precisão razoável, mas não os componentes individuais compondo. \(x^c\) relaciona-se às propriedades da nuvem e \(\bar{x}\) às propriedades médias do ambiente. As diferenças entre os esquemas de parametrização está principalmente na forma de cálculo de \(M^c\). M é proporcional à densidade e à fração de área coberta por nuvens.
A teoria de quasi-equilibrium, apresentada pela primeira vez por Arakawa e Schubert (1974), basicamente afirma que a atividade convectiva (estabilização) está em quase-equilíbrio com a forçante em grande escala (desestabilização) da atmosfera, de modo que a taxa de variação resultante no CAPE é pequeno. Assim, ela fornece uma descrição simplificada, mas tratável, da interação geral entre a convecção e o ambiente em grande escala.
O entranhamento é entrada de ar do ambiente na parcela, sendo o parâmetro mais importante em uma parametrização de convecção de fluxo de massa. As taxas de entranhamento e “desentranhamento” são expressas como uma soma de contribuições combinadas (“mixing”) e organizadas (“organized”). As contribuições combinadas derivam de uma formulação de Simpson (1983) que expressa a taxa de entranhamento fracionária como sendo inversamente proporcional ao raio da nuvem. Com isso em mente, os valores típicos implicam em um raio médio de corrente ascendente na base da nuvem de aproximadamente 100 metros para convecção profunda e de 50 metros para convecção rasa, implicando em um entranhamento bastante forte. Também pode-se incluir funções de escala vertical para imitar o efeito de um conjunto de nuvens. Como a função de escala diminui fortemente com a altura, o desentranhamento da mistura eventualmente se tornará maior do que o entranhamento e o fluxo de massa começará a diminuir com a altura. A taxa de entranhamento é ainda modulada pela umidade relativa do ambiente.
Um problema de fechamento é a determinação do fluxo de massa na base da nuvem para determinar a magnitude geral do aquecimento (ou seja, precipitação superficial em convecção profunda). Os tipos de fechamento para convecção profunda assumem um equilíbrio que se estabelece em uma escala de tempo típica de uma hora entre a produção do CAPE pela grande escala e seu consumo pela convecção.
Alguns esquemas também usam algum tipo de ajuste CAPE para convecção rasa mas com uma escala de tempo de ajuste mais longa, normalmente de três horas. Em um tipo de fechamento de equilíbrio simples, o fluxo de massa convectiva da base da nuvem é proporcional ao produto da fração de elevação e da velocidade vertical, sendo a última proporcional à camada limite ou altura da base da nuvem e ao fluxo de flutuabilidade.
A primeira etapa do algoritmo de convecção consiste na seleção de colunas convectivas. Primeiro teste para convecção rasa envolve adicionar uma perturbação (na temperatura ou umidade) para mudar a magnitude dos fluxos de superfície para uma parcela de ar próxima à superfície. Estando a subida com forte entranhamento, deve-se verificar se há LCL (Lifting Condensation Level), calcular o empuxo e continuar subindo até que o CTL (Cloud Top Level) seja alcançado, que é definido como empuxo negativo. Se o empuxo no LCL for maior que zero e a diferença de pressão entre CTL e LCL for menor que 200 hPa, a convecção superficial deve ocorrer – caso contrário, convecção profunda.
Com relação à parametrização de microfísica, veja no post Nuvens e precipitação em escala de grade.