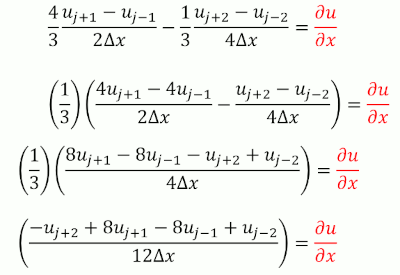As principais fontes de erros nas soluções numéricas, além de erros como os devidos à estabilidade de discretização e à escolha do método numérico, são o Round-off e o Truncamento.
O erro de Round-off costuma ser o menos importante mas ganha importância na soma de números pequenos com números grandes – especialmente quando se está em forma de acúmulos de somas. Para evitar esse problema, é uma boa prática o uso de variáveis de precisão dupla.
O erro de Truncamento é gerado quando funções contínuas são representadas por uma série de valores pontuais. De modo geral, esse erro tende a diminuir quanto mais valores de ponto de grade forem utilizados para aproximar a função – conforme a função, varia a resolução necessária para reduzir o erro de truncamento para um nível aceitável.
De modo geral, quanto maior a ordem da discretização de uma derivada espacial, melhor a acurácia da aproximação. No entanto, aumentando a ordem do erro de truncamento, isso não elimina os artefatos numéricos gerados pelo modo computacional, e uma das formas de amortecer esses ruídos é através dos filtros.
Exercício – Resolva numericamente a equação de advecção utilizando a acurácia de quarta ordem na discretização espacial e compare com a solução de segunda ordem. Considere \(\mu =\frac{c\Delta x}{\Delta t}=0.2\) e \(\mu =\frac{c\Delta x}{\Delta t}=0.7\). Como condição inicial use uma onda quadrada.
Resolução
A equação de advecção pode ser representada conforme segue:
O script EDP_Advec.f90 contém as funções “Solve_Inst_FTCS” (acurácia de 2ª ordem) e “Solve_Instavel_4thCS” (acurácia de 4ª ordem) que resolvem numericamente uma função de onda quadrada, resolvida analiticamente na função “AnaliticFunction”. Todas são chamadas na “SUBROUTINE Run”, mas primeiramente a função com acurárcia de 2ª ordem está descomentada.
Como padrão, estavam definidas as seguintes constantes (critério de estabilidade), que correspondem a \(\mu=0.36\):
DeltaX=1.0 DeltaT=0.55 C =0.2
Para usar os valores de \(\mu\) solicitados no exercício, foram alterados os valores de \(\Delta t\) mantendo o resto constante. Assim, para \(\mu=0.2\) temos \(\Delta t=1\) e para \(\mu=0.7\) temos \(\Delta t=0.29\). Inicialmente, foi definido “DeltaT=1.0”.
Foram utilizados os seguintes comandos para compilar o código e executá-lo (com as respectivas saídas):
$ gfortran EDP_Advec.f90 $ ./a.out DeltaX= 1.0000000000000000 DeltaT= 1.0000000000000000 CFL= 0.20000000298023224 err= 5.7464488003074636E+047 DeltaX= 1.0000000000000000 DeltaT= 1.0000000000000000 CFL= 0.20000000298023224
Foi gerado um arquivo binário e um CTL, que foram renomeados para 2a_ordem.bin e 2a_ordem.ctl (o arquivo CTL teve sua referência ao arquivo “AdvecLinearConceitual1D” alterada para “2a_ordem” em seu interior também).
Então o script EDP_Advec.f90 foi alterado para chamar a função “Solve_Instavel_4thCS” (em vez de “Solve_Inst_FTCS”) dentro da “SUBROUTINE Run”. O mesmo procedimento foi adotado, sendo que as renomeações foram para “4a_ordem”.
DeltaX= 1.0000000000000000 DeltaT= 1.0000000000000000 CFL= 0.20000000298023224 err= 5.7443748321195783E+090 DeltaX= 1.0000000000000000 DeltaT= 1.0000000000000000 CFL= 0.20000000298023224
Os arquivos CTL (referenciando os respectivos arquivos binários) foram abertos no grads para visualização gráfica usando os seguintes comandos (com as respectivas saídas):
ga-> open 2a_ordem.ctl
Scanning description file: 2a_ordem.ctl
Data file 2a_ordem.bin is open as file 1
LON set to 0 999
LAT set to -1.27 -1.27
LEV set to 1000 1000
Time values set: 1:1:1:0 1:1:1:0
E set to 1 1
ga-> q file
File 1 : EDO
Descriptor: 2a_ordem.ctl
Binary: 2a_ordem.bin
Type = Gridded
Xsize = 1000 Ysize = 1 Zsize = 1 Tsize = 3000 Esize = 1
Number of Variables = 2
uc 0 99 resultado da edol yc
ua 0 99 solucao analitica ya
ga-> open 4a_ordem.ctl
Scanning description file: 4a_ordem.ctl
Data file 4a_ordem.bin is open as file 2
ga-> q file
File 1 : EDO
Descriptor: 2a_ordem.ctl
Binary: 2a_ordem.bin
Type = Gridded
Xsize = 1000 Ysize = 1 Zsize = 1 Tsize = 3000 Esize = 1
Number of Variables = 2
uc 0 99 resultado da edol yc
ua 0 99 solucao analitica ya
ga-> set vrange -1 2
1-D axis limits set: -1 to 2
ga-> set t 50
Time values set: 1:1:3:1 1:1:3:1
ga-> d ua
ga-> d uc.1
ga-> d uc.2
Assim, definido o tempo 50, obtém-se o seguinte gráfico:
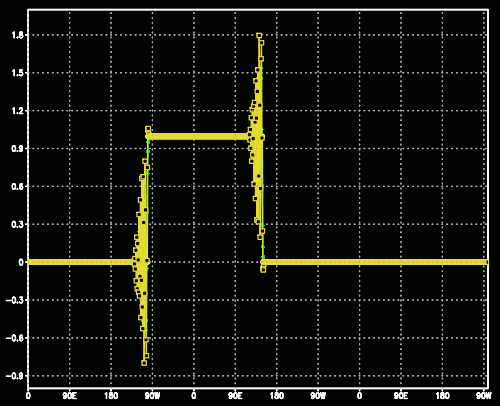
Quando se usa o método centrado no espaço para discretização, em tese melhoraria a solução aumentando-se a ordem de truncamento. No entanto, aumentando a ordem do erro de truncamento, isso não elimina os artefatos numéricos gerados pelo modo computacional. Uma das formas de amortecer esses ruídos é através dos filtros. Em nenhuma das soluções apresentadas foi utilizado filtro.
O mesmo procedimento foi repetido para \(\mu=0.7\) (DeltaT=0.29), gerando a seguinte saída (e gráfico) para 2ª e 4ª ordens:
DeltaX= 1.0000000000000000 DeltaT= 0.28999999165534973 CFL= 5.7999999195337271E-002 err= 495.25792039818867 DeltaX= 1.0000000000000000 DeltaT= 0.28999999165534973 CFL= 5.7999999195337271E-002 DeltaX= 1.0000000000000000 DeltaT= 0.28999999165534973 CFL= 5.7999999195337271E-002 err= 937380.75108861446 DeltaX= 1.0000000000000000 DeltaT= 0.28999999165534973 CFL= 5.7999999195337271E-002

Comparando-se com o obtido agora com o \(\mu\) de valor menor, nota-se que o ruído foi bem menor para as mesmas condições. Esse resultado era esperado devido à redução do passo de tempo.
Método de Runge-Kutta
O método de Runge-Kutta é usado para a resolução numérica de soluções de equações diferenciais ordinárias. Uma das formas para desenvolver uma solução aproximada é expandindo uma solução y(t) em série de Taylor próximo de uma condição inicial (t = 0).
Restringindo a solução para um intervalo de tempo curto (h) após t = 0 e truncando a série de Taylor após a primeira derivada, o valor da aproximação é dito y*(h) e a derivada é y′(0) = k1. Para encontrar o valor da aproximação após a próxima etapa de tempo, y*(2h), repete-se o processo usando a aproximação y*(h) para estimar a derivada no tempo h (k1).
Assim, com relação ao método de Runge-Kutta de 1ª ordem (método de Euler), para uma equação diferencial ordinária de primeira ordem definida por dy(t)/dt = f(y(t),t) progredir de um ponto em t = t0, y*(t0), por um intervalo de tempo h, deve seguir essas etapas (repetidamente): aproximação para derivada k1 = f(y*(t0),t0) e solução aproximada para o próximo passo y*(t0+h) = y*(t0+k1h).
Sobre o método de Runge-Kutta de 2ª ordem, o conceito central é repetido. O valor inicial da função fornecido para iniciar o algoritmo é frequentemente chamado como o “ponto médio” (ou “midlepoint”) para Runge-Kutta de segunda ordem porque usa a inclinação no ponto médio, k2.
Assim como a técnica de 2ª ordem, existem muitas variações do método de 4ª ordem, e todos eles usam quatro aproximações para o declive. A inclinação no início do intervalo de tempo é k1 (o mesmo usado nos métodos de 1ª e 2ª ordem). Usando k1 para avançar na metade do intervalo de tempo, então k2 é uma estimativa da inclinação no ponto médio (o mesmo usado no método de 2ª ordem). Usando a inclinação k2 para avançar na metade do intervalo de tempo, então k3 é outra estimativa da inclinação no ponto médio. Finalmente, usando a inclinação k3 para percorrer todo o caminho através da etapa de tempo (para t0 + h), k4 é uma estimativa da inclinação no ponto final (“endpoint”). Assim, a estimativa de y(h) fica:
\(y*(h)=y(0)+\frac{k_1+3k_2+2k_3+k_4}{6} h\)
Uma implementação do esquema de discretização de Runge-Kutta de 2ª, 4ª e 6ª ordem em Fortran 90 e comparação dos resultados ao aproximar numericamente a resolução de uma onda quadrada pode ser visto no github: viniroger/runge-kutta.