Conheça uma versão FORTRAN 77 do pioneiro modelo numérico de previsão de tempo de Richardson, após uma breve recapitulação dos principais fatos históricos na evolução da área. Desde a pré-história, o ser humano observa a natureza e faz especulações na tentativa de prever o comportamento da atmosfera. No entanto, o conhecimento do tempo passado e presente, assim como as propriedades atmosféricas devem evoluir no tempo, é algo que pode ser modelado usando matemática, física e computação.

No século 18, descobertas na área da Matemática, como o cálculo diferencial, e da Física, como as leis de dinâmica, possibilitaram ferramentas teóricas para fundamentar a Meteorologia no século seguinte. Avanços foram feitos na área de dinâmica dos fluidos e termodinâmica, com as equações de Navier-Stokes e de estado dos gases (trabalhos do inglês Lorde Kelvin e do alemão Hermann von Helmholtz).
Um modelo conceitual descreve um processo com o objetivo de apresentar um conceito e obter as regras gerais de funcionamento do mundo real, através de simplificações e assumindo aproximações em pontos de menor importância para o conjunto estudado. Por exemplo, a Teoria da Frente Polar proposta por Jacob Bjerknes em 1919 é um modelo conceitual onde mostrava que, durante o processo de convergência dos ventos em superfície, o ar quente (menos denso) sobe sobre o ar frio.
Um modelo matemático é baseado em um modelo conceitual, mas deve conter um conjunto de equações para descrever quantitativamente um processo. Por exemplo, as equações primitivas da atmosfera: Segunda lei de Newton (Equação do Movimento), Equação do gás ideal (Equação de Estado) e Primeira lei da termodinâmica (Equação da Termodinâmica). Sua implementação em um computador é o modelo numérico, como os códigos dos modelos de previsão de tempo e clima.
Os primeiros modelos físico-matemáticos de ciclones e frentes foram elaborados, com destaque para os trabalhos do estadunidense Cleveland Abbe (1901) e do norueguês Vilhelm Bjerknes (1904). Eles definiram que a previsão de tempo é um problema determinístico de valor inicial, ou seja, usando condições iniciais e equações governantes.
Max Margules e Felix Maria Exner publicaram estudos relacionados, respectivamente, à tendência da pressão através da equação de continuidade e a princípios físicos para calcular mudanças sinóticas. Foram as primeiras tentativas em usar princípios físicos para calcular mudanças em grande escala.
As bases teóricas melhoraram entre as décadas de 1920 e 1950. Na Meteorologia dinâmica, foram desenvolvidos os conceitos das ondas de Rossby, a Teoria quase-geostrófica e a instabilidade baroclínica, além do descobrimento da circulação em altos níveis.
O avanço de métodos numéricos, como das diferenças finitas, permitiram a resolução de equações diferenciais parciais não lineares, que não possuem solução analítica. O trabalho de Courant, Friedrichs e Lewy (1928) gerou o CFL, um parâmetro de cálculo que modifica a magnitude local do Número de Courant, que por sua vez é uma grandeza escalar local do domínio fluido que representa o fluxo advectivo em cada volume finito. A Condição CFL é o intervalo de CFL que permite a precisão física e estabilidade do cálculo, relacionando espaçamento de grade e passo de tempo. Essa condição é necessária mas não suficiente, já que a instabilidade não linear e arredondamentos podem inserir problemas.
Deve-se evitar o aliasing, em que instabilidades não lineares crescem ao infinito, formadas por eventos de grande escala criando ondas menores e artificiais. O jacobiano de Arakawa conserva a energia, a vorticidade e a enstrofia (energia cinética no fluxo que corresponde aos efeitos de dissipação no fluido), cortando a transferência de energia da grande para a pequena escala. Segundo o teorema de Lax-Ritchtmeyer, se a solução discretizada de uma equação diferencial é consistente (erro de discretização tende a zero) e estável, ela é convergente.
Foram desenvolvidos diferentes métodos para cálculo usando sistemas discretos. No método explícito, calcula-se o estado do sistema em um tempo posterior ao estado atual, havendo restrições no passo de tempo. No método implícito, encontra-se a solução resolvendo uma equação que envolve tanto o estado atual quanto o posterior, tendo como vantagem ser incondicionalmente estável e permitindo um passo de tempo grande. Já o método semi-implícito separa termos lentos (como ondas de Rossby, em que é necessário um passo de tempo menor) e mais rápidos (como ondas de gravidade, onde pode aumentar o passo de tempo) em métodos explícito e implícito, respectivamente.
Somente com os computadores eletromecânicos que foi possível fazer a primeira previsão numérica de tempo (PNT) mais bem sucedida. Em 1950, o ENIAC (Electronic Numerical Integrator and Computer) fez a previsão para as próximas 24 hores em 24 horas – não é operacional mas é um começo. Os principais responsáveis foram Charney, Fjortoft e Neuman, entre 1948-49.
Com a Segunda Guerra Mundial, houve uma sistematização da Previsão do Tempo. As observações meteorológicas também melhoraram, com o uso de radares, radiossondas (1940) e de satélites (1960). Mudanças nos modelos com relação a malha, regional a global (1974) e diferenças finitas a espectral (1980) vieram também na melhoria da PNT.
Modelo numérico de previsão de Richardson
O inglês Lewis Fry Richardson (1881-1953) sonhava que a previsão do tempo científica um dia se tornaria uma realidade prática. No No início do século 20, essa iniciativa era muito desacreditada. Isso porque vários avanços foram necessários para torná-la viável: melhor compreensão da dinâmica da atmosfera; algoritmos computacionais estáveis para integrar as equações; observações regulares da atmosfera livre; e equipamentos de informática automáticos potentes.
Richardson descreveu um método para integrar numericamente as equações que governam a atmosfera: de movimento, termodinâmica e de continuidade. Entre 1916 e 1922, fez um experimento quando da passagem do cometa Halley (7 UTC, 20 maio de 1910) em 200 km, 4 camadas com 200 hPa cada uma, sobre a Alemanha, com cálculos manuais de vários meses para análises de pressão ao nível do mar e geopotencial em 500 hPa.
No livro “The Emergence of Numerical Weather Prediction: Richardson’s Dream“, o autor Peter Lynch conta a história da primeira tentativa de cálculo e inclui uma reconstrução completa da previsão de Richardson. Em sua página, Lynch disponibiliza um arquivo compactado contendo uma seleção de código FORTRAN 77 escrito por ele mesmo, que implementa o modelo baroclínico de Richardson da atmosfera. Os dados iniciais baseados em observações para 0700Z, 20 de maio de 1910 também estão incluídos:
- OROG.DAT – altitude em metros (orografia)
- PS.DAT – pressão em superfície (mm Hg X 10)
- T.DAT – espessura da camada de 200-100mb, para temperatura
- UV.DAT – velocidade e direção do vento (100, 300, 500, 700 e 900 mb)
- Z.DAT – altura geopotencial (200, 400, 600 e 800 mb)
O arquivo a ser compilado é o “richie.f” com outros arquivos “.f” de sub-rotinas. Pode rodar o executável como “richie.x > richie.lpt” para capturar a saída. O arquivo “richie.cds” contém as informações de inicialização do modelo. Por padrão, ele integra o modelo por 24 horas (variável “tEnd”).
A rodada original de Richardson obteve uma tendência da pressão no valor de 145.4 mb/6h. É um valor muito fora da realidade física – para se ter uma ideia, um ciclone bomba teria uma queda de aproximadamente 6 mb nesse mesmo período. Nessa caso, o arquivo “richie.cds” usa valores negativos para as variáveis “Timestep” e “tEnd”, ou seja, sem inicialização.
Essa inicialização atua como um ajustamento de massa e movimento, importante para a dinâmica do modelo. Isso ocorre devido à influência de ondas de alta frequência (como ondas acústicas e de gravidade) nas condições iniciais, que devem ser filtradas para que tudo fique em balanço.
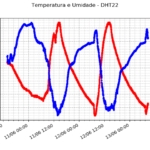
No primeiro passo temporal de uma rodada sem inicialização, os valores de “Pressure Tendency” impressos no arquivo de log começam em 145.4 mb/6h. A tendência de pressão verdadeira (“True Pressure Tendency” no arquivo log) foi de 211.5 mb/6h, variando para valores de módulo menor (tanto negativos quanto positivos) mas ainda muito grandes para serem fisicamente possíveis nos passos seguintes. A tendência de pressão oscilou entre valores cada vez menores até estabilizar em um valor mais próximo da realidade, conforme gráfico a seguir:

O tempo que o modelo demora para estabilizar, com resultados inconsistentes, é conhecido como “spin-up”. O fato de estabilizar em um valor garante que a solução é estável. Como nessa época não se conhecia das condições CFL de estabilidade, o modelo ia estourar com o passo de tempo utilizado por Richardson – nessa rodada, foi utilizado passo de 300 segundos, que é garantido que o modelo não vai estourar se continuar integrando.
Para considerar o filtro de inicialização, usam-se variáveis positivas, como ‘Timestep = +300’ e ‘tEnd = +01.5’ – como estabiliza com poucos passos de tempo, não precisa integrar por 24h pra essa análise.
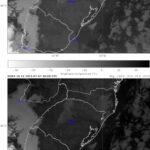
Nas condições iniciais, a diferença com e sem filtro dos valores da tendência de pressão é grande, conforme pode-se observar na figura a seguir:
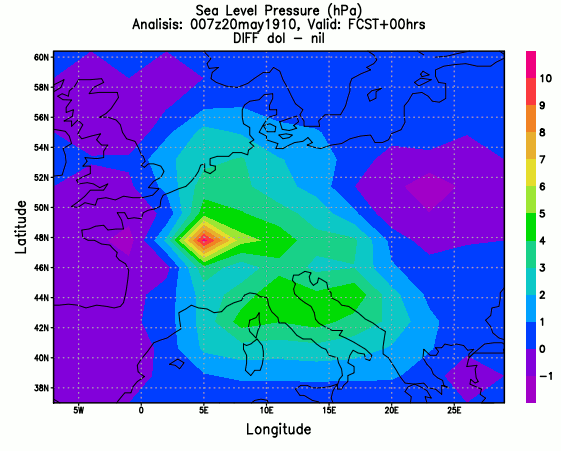
No modelo com filtro digital, as oscilações iniciais são menores e a estabilidade ocorre mais rapidamente. O filtro suaviza os valores das condições iniciais, evitando picos. Por exemplo, observando-se o campo inicial de pressão à superfície nos arquivos de log, quando não é aplicado o filtro, existe um valor destacado de 998 mb que não aparece no primeiro campo do arquivo de log quando o modelo roda com inicialização, que por sua vez tem uma aparência mais suave. Dessa forma, podem ser gerados valores de tendência de pressão mais condizentes com a realidade.
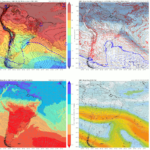
As diferenças de pressão nos cenários previstos com (dol) e sem filtro (nil) mantêm-se espacialmente nas mesmas regiões, com os maiores valores sobre a região da Alemanha. Na previsão de 24 horas, as diferenças diminuem de uma ordem de grandeza se comparadas com a previsão de 12 horas. Com as outras variáveis (u – zonal wind, v – meridional wind, mu – momenta, mv – momenta, ttop), também acontecem redução na diferença entre os cenários com e sem filtro.

Os tipos de malha, discretização Métodos numéricos para modelagem atmosférica. Uma discussão maior a respeito de erros numéricos e de filtros pode ser vista no post de Erros de soluções numéricas e Runge-Kutta. Sobre parametrização de nuvens e precipitação, veja também o post Nuvens e precipitação em escala de grade.
Diferenças entre modelos de tempo, de clima, globais e regionais
Um sistema de Previsão Numérica de Tempo e Clima tem como componentes:
- Aquisição de dados: observações em centros de dados, como GTS (Global Telecommunication System), satélite, etc
- Pré-processamento: controle de qualidade, comparar com o modelo global e seleção de área
- Análise (dinâmica e estatística): assimilação de dados (podem ser misturados dados observados e interpolados para corrigir saída do modelo com “first guess”)
- Modelo: recebe a inicialização, que deve ter uma suavização de ondas de alta frequência para não gerar previsões artificiais, e gera o “first guess” do modelo
- Pós-processamento: converter dados para latitude e longitude, calcular índices derivados
- Disseminação: publicação em rede dos resultados para consulta
Dentro do modelo numérico, entram a condição inicial, que deve conter dados de qualidade para bons resultados; o conjunto de equações governantes, que devem descrever os processos físicos da melhor forma possível na escala de trabalho; e os métodos de discretização para resolução das equações em algoritmos computacionais, de modo que as aproximações reflitam um mínimo de erros mas sem inviabilizar a divulgação das previsões em um prazo operacional.
Na previsão numérica de tempo, as mudanças do dia-a-dia na circulação atmosférica em grande escala não são previsíveis além de duas semanas. No entanto, as médias de espaço-tempo de certas variáveis atmosféricas e oceânicas são previsíveis de meses a estações. A base científica para a previsão sazonal reside na interação da atmosfera com componentes do sistema climático que variam lentamente – principalmente os oceanos e a superfície terrestre. Desse modo, a previsão de clima tem uma estatística entrelaçada com as variáveis adotadas visando prever semanas e meses a frente.
As mudanças climáticas atuais observadas são uma combinação de influências antropogênicas e da variabilidade natural. Além da possível influência antrópica no clima devido à mudança na composição atmosférica (incremento de gases de efeito estufa, por exemplo), a mudança de uso do solo leva a mudanças significativas nas propriedades biofísicas da superfície terrestre, como albedo e umidade do solo. Assim, a mudança dessas variáveis no tempo devem ser incluídas em modelos que visam prevem o clima após algumas décadas.
Os modelos globais apresentam maior horizonte de previsão e cobrem uma área maior que os regionais, mas possuem menor resolução espacial para gerarem previsões em tempo hábil – seria necessário muito processamento e espaço de armazenamento também. BAM (Brazilian Global Atmospheric Model) é o modelo global operacional do CPTEC. Ele tem resolução espacial de 20 quilômetros e 96 camadas na vertical, com horizonte de previsão de até 15 dias. É um modelo espectral hidrostático com difusão horizontal semi-implícita e coordenada vertical sigma (Figueroa, 2016).
Os modelos regionais, ao trabalharem com uma resolução maior, também devem modelar fenômenos de menor escala e desconsiderar aproximações que são feitas em modelos globais. O WRF (Weather Research and Forecasting) é usado operacionalmente no CPTEC como modelo regional. Tem resolução espacial de 5 quilômetros e 31 camadas na vertical, com horizonte de previsão de até 72 horas. Sua estrutura vertical é resolvida através de coordenada Eta (Ramos, 2020).
Habilidade de previsão de tempo
E. Lorenz (1965) forneceu um modelo conceitual simples no qual o limite superior da habilidade de previsão do tempo é descrito por três quantidades fundamentais: o tamanho do erro inicial, a taxa de crescimento do erro e o valor de saturação do erro. A definição clássica de Lorenz para previsibilidade do tempo relaciona o intervalo no qual a diferença entre as previsões de duas condições iniciais quase idênticas é tão grande em um sentido estatístico quanto a diferença entre dois estados atmosféricos escolhidos aleatoriamente. Com isso, fica implícito que o limite superior da previsibilidade depende do valor de saturação do erro máximo possível, que, por sua vez, é determinado pela variância climatológica.
O inverno é mais previsível do que o verão, e as latitudes médias são mais previsíveis do que os trópicos. Isso ocorre porque o valor de saturação do erro de previsão é muito maior no inverno e nas latitudes médias do que nos trópicos. Nas estações do ano de transição (primavera e outono), os modelos tendem a ter menos sucesso do que no verão ou inverno devido ao crescimento da variância das flutuações no período.
Nos trópicos, a variância das flutuações diárias e, portanto, de saturação dos erros, é muito menor do que nos extratrópicos (Shukla, 1981). No entanto, a taxa de crescimento do erro nos trópicos, dominada por instabilidades associadas à convecção, é maior do que nos extratrópicos, onde o crescimento do erro está principalmente associado à instabilidade baroclínica (Schukla & Kinter III, 2006). Assim, o limite superior da previsibilidade determinística nos trópicos é menor do que nos extratrópicos. Além disso, as ondas longas, dominantes nos extratrópicos, são mais previsíveis do que as ondas curtas, principalmente devido ao maior valor de saturação dos erros para as ondas longas do que para as ondas curtas. Em contraste, as flutuações climáticas de curto prazo nos trópicos são dominadas pelas condições de contorno que variam lentamente, então as médias sazonais nos trópicos são mais previsíveis do que as extratropicais.
Referências
Notas de aula de MET 348 – Previsão Numérica de Tempo e Clima (pós-graduação em Meteorologia/INPE)
The Emergence of Numerical Weather Prediction: Richardson’s Dream by Peter Lynch
Figueroa, S. N. et al. The Brazilian Global Atmospheric Model (BAM): performance for tropical rainfall forecasting and sensitivity to convective scheme and horizontal resolution. Weather and Forecasting, v. 31, n. 5, p. 1547–1572, 2016.
Ramos, D. N. da S. et al. Avaliação Preliminar Do Modelo Wrf-Solar Para Previsão Das Irradiâncias Global Horizontal E Direta Normal. VIII Congreso Brasileiro de Energia Solar – CBENS. Anais…Fortaleza, Ceará, Brazil: Associação Brasileira de Energia Solar, 2020
Lorenz, E. N. (1965). A study of the predictability of a 28-variable model. Tellus, 17, 321–33.
Shukla, J. (1981). Dynamical predictability of monthly means. J. Atmos. Sci., 38, 2547–72.
Schukla, J., Kinter III, J. L. (2006) Predictability of seasonal climate variations: a pedagogical review. In: Palmer, Hagedorn (Eds.) Predictability of Weather and Climate. Cambridge University Press pp. 306, chapter 12.