Modelo ARIMA

Existem modelos que são uma descrição probabilística de uma série temporal. Muito utilizado na modelagem e previsões de séries temporais, o modelo ARIMA foi sistematizado em 1976 pelos estatísticos George Box e Gwilym Jenkins. Seu nome deriva do inglês autoregressive integrated moving average, que significa modelo autorregressivo integrado de média móvel. Para ver alguns conceitos mais básicos sobre Estatística, clique no link.

Em estatística, regressão é uma técnica que permite explorar e inferir a relação de uma variável dependente Y (variável de resposta ou exógena) com uma (X) ou mais variáveis independentes específicas (variáveis explicatórias ou regressoras ou endógenas). Pode ser usada como um método descritivo da análise de dados (como, por exemplo, o ajustamento de curvas) sem serem necessárias quaisquer suposições acerca dos processos que permitiram gerar os dados.

O método de estimação mais amplamente utilizado é o método dos mínimos quadrados ordinários (MMQ ou MQO) – técnica de otimização matemática que procura encontrar o melhor ajuste para um conjunto de dados tentando minimizar a soma dos quadrados das diferenças entre o valor estimado e os dados observados (tais diferenças são chamadas resíduos). A curva resultante é denominada de regressão de Y para X, sendo Y avaliado a partir de X. Uma boa planilha para praticar esse ajuste está disponível no STOA da matéria de Física Experimental: ajuste_de_reta.ods.

Para calcular previsões de séries temporais com um grande número de observações, é razoável aceitar o ajuste de modelos autorregressivos. Se o número de dados for pequeno, essa análise não é apropriada, pois a hipótese básica de independência dos resíduos é quase sempre violada, gerando estimadores inconsistentes. Nesse caso, os métodos de alisamento são mais utilizados. Alternativamente, pode-se utilizar a técnica de filtragem adaptativa, que não faz discriminação entre ruído e padrão básico – sua hipótese básica é que o padrão de comportamento da série possa ser representado por uma soma ponderada de observações passadas.

Suponha que a variável aleatória y é linearmente relacionada com seus próprios valores defasados. Na forma mais geral da análise de regressão, a variável dependente transformada pode ser explicada por variáveis independentes também transformadas:

A hipótese de trabalho por trás da transformação é equivalente à afirmativa de que existe algum valor de λ para o qual y^λ tem distribuição (aproximadamente) normal com média dada pelo produto vetorial β’X e variância constante. Para λ = 1, a transformação deixa a variável praticamente inalterada, e para λ = 0 implica na transformação logarítmica da variável.

Como o parâmetro da transformação (λ) é desconhecido, deve-se estimá-lo a partir dos dados da amostra. Isso torna o modelo não-linear nesse parâmetro e exige a utilização do método de máxima verosimilhança para se obter estimadores com propriedades desejáveis. Após realizar a padronização da variável de resposta y é possível transformá-la, segundo Box–Cox, com diferentes valores de λ, ajustar as várias regressões por MQO, e escolher aquele valor do parâmetro para o qual a soma dos desvios quadráticos seja mínimo. Existem alguns pacotes computacionais que realizam essas estimativas escolhendo o λ ótimo de maneira automática e fornecendo a estatística necessária para realizar testes de significância da estimativa desse parâmetro de transformação.

Na análise de modelos paramétricos, existe o método de Box & Jenkins, que consiste em ajustar modelos autorregressivos integrados médias móveis (ARIMA) a um conjunto de dados. Sua estratégia para a construção do modelo é baseada em um ciclo iterativo (a escolha do modelo é baseada nos próprios dados), cujos estágios são:

1. Especificação – uma classe geral de modelos é considerada para análise (ARIMA, no caso);
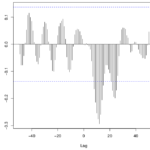
2. Identificação de um modelo com base na análise de autocorrelações e autocorrelações parciais;
3. Estimação dos parâmetros do modelo identificado (as estimativas preliminares encontradas na fase de identificação serão usadas como valores iniciais nesse procedimento);
4. Verificação do modelo ajustado através de uma análise de resíduos (menor erro quadrático médio) para saber se este é adequado para os fins (no caso, de previsão).

Caso o modelo não seja adequado, o ciclo é repetido. O procedimento de identificação para determinar os valores de p, d e q do modelo ARIMA(p,d,q) envolve: verificar se precisa de transformação não linear (como a transformação Box-Cox, que muda a série exponencial para linear), eventualmente tomar diferenças para deixar a série estacionária (valor d) e encontrar o ARMA (valores p e q).

O principal argumento utilizado para a modelagem é uma série temporal univariada (“univariate time series”). Uma série temporal consiste de observações únicas (escalares) registradas sequencialmente durante incrementos iguais de tempo, enquanto que a palavra “univariada” implica que há somente uma variável dependente – ou seja, existe uma função y = f(t) tal que t é a variável independente e y a variável dependente (de t, que no caso representa o tempo). Quando os valores da série podem ser escritos através de uma função desse modo, diz-se que a série é determinística – caso envolva também um termo aleatório, a série é chamada estocástica.

Uma série estacionária (ou convergente) flutua em torno de uma mesma média ao longo do tempo (a sequência de suas somas parciais convergem), diferentemente da série não estacionária (ou divergente), onde ocorrem tendências ascendentes e descendentes. Suas propriedades não dependem do momento em que foi observada. Para tornar a série estacionária deve-se tomar diferenças quantas vezes for necessário, até atingir estacionariedade – são chamadas de séries não estacionárias homogêneas. Um modelo é estacionário se, para todo t, tem-se os valores de média, variância e covariâncias constantes. Por exemplo, quando a série oscila ao redor de um nível e salta para outro, basta uma diferença para torná-la estacionária; se a série oscila em uma direção e depois muda, são necessárias duas diferenças para ficar estacionária.

O modelo autorregressivo de ordem p é usado quando há autocorrelação entre as observações, ou seja, quando o valor de uma variável no período t depende do seu valor no período anterior (t-1) e de um termo aleatório. O modelo de média móvel de ordem q é usado quando há autocorrelação entre os resíduos – de modo geral, quanto maior o número de termos que compõe a média móvel, mais suavizado fica. Já o modelo autorregressivo de média móvel (ARMA) é usado quando há autocorrelação entre as observações e autocorrelação entre os resíduos. Um modelo AR (1) é apenas um coeficiente vezes o valor atrasado, além do ruído branco; um modelo MA (1) é apenas um coeficiente de vezes o valor defasado do ruído branco, além do ruído branco; um ARMA (1,1) é uma combinação dos dois.

Se o modelo ARMA(p,q) é uma diferença da série temporal Zt, então essa série temporal é uma integral do modelo, daí temos que Zt segue um modelo autorregressivo-integrado-médias móveis (ARIMA).

Considere uma série temporal escrita da seguinte forma:

\(Z_t=f(t)+a_t\), t = 1,…,N

\(f(t)=T_t+S_t\) (se S_t independe de T_t) ou \(f(t)=T_t.S_t\) (caso contrário)

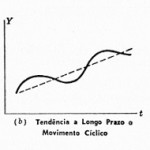
A função f(t), chamada “sinal”, é composta da adição/multiplicação da componente ciclo-tendência (Tt), que inclui as flutuações cíclicas de longo período que não podem ser detectadas com os dados disponíveis, e da componente sazonal (St), enquanto que at é o “ruído aleatório”. Pode-se considerar duas classes de modelos: modelos de erro ou de regressão, onde o sinal f(t) é uma função do tempo completamente determinada de observações independentes e at é uma sequência aleatória independente de f(t), e modelos ARIMA. A hipótese de erros não correlacionados introduz limitações na validade dos modelos que seguem equações do tipo apresentado acima. Para descrever o comportamento de séries onde os erros observados são correlacionados e influenciam a evolução do processo, são utilizados os modelos ARIMA.

O modelo ARIMA é dado em função de p, q e d:

Onde:

• p é o número de termos autorregressivos;
• d é o número de diferenças;
• q é o número de termos da média móvel;
• L é o operador defasagem;
• Φ é o polinômio ligado ao operador autorregressivo de ordem p;
• θ é o polinômio ligado ao operador de média móveis de ordem q;
• εt (ou at) é o ruído branco (sinal discreto cujas amostras são vistas como uma sequência de variáveis aleatórias não auto-correlacionadas com média zero e variância finita).

Para d = 0, tem-se o modelo ARMA(p, q), e no caso de também q = 0, tem-se o modelo AR(p) – o modelo ARIMA(0, 1, 0) é o passeio aleatório (random walk). A parte autorregressiva do modelo prediz o valor no momento t, considerando valores anteriores nas séries no momento t-1, t-2, etc. A média móvel usa valores de resíduos passados (as diferenças entre o valor real e o valor predito baseado no modelo no momento t).

O vídeo abaixo explica esse modelo com mais detalhes e exemplos:

O modelo SARIMA (sazonal autoregressivo integrado de médias móveis) trata séries que não têm estacionariedade, mas possuem periodicidade cíclica, com picos e declínios no decorrer de sua evolução temporal. A série diferenciada com ordens d e D, sendo D a “ordem de diferenciação sazonal”. Sua ordem é dada por (p,d,q)x(P,D,Q)_S, onde S é o período. Outra generalização é o (S)ARIMAX, que incorpora um componente linear em função das observações das covariáveis (ou regressores ou preditores) – veja mais no post sobre Regressão múltipla.

Interpretação dos critérios

Os modelos ARIMA são mais eficientes em situações que envolvem um pequeno número de séries temporais – comprimento entre 50 (mínimo) e 100 observações (Montgomery, 1990). Na escolha do modelo mais apropriado, busca-se o que for mais parcimonioso, ou seja, que envolva o mínimo de parâmetros possíveis a serem estimados e que explique bem o comportamento da variável resposta.

A verossimilhança (ou likelihood, em inglês) é uma característica de algo que é semelhante à verdade, provável. Em estatística, a noção de verossimilhança é uma função da probabilidade condicional (probabilidade de um evento A sabendo que ocorreu um outro evento B). Deve-se escolher o valor do parâmetro desconhecido que maximiza a probabilidade de obter a amostra particular observada, ou seja, o valor que torna aquela amostra a “mais provável”. Assim, ao obter a função de verossimilhança, que depende dos parâmetros desconhecidos e dos valores amostrais, deve-se maximizar essa função (derivar a função e igualar a zero para encontrar o ponto de máximo) ou o logaritmo de base “e” dela, o que for mais conveniente (Morettin & Bussab, 2004).

Existem estimadores (também chamados ‘critérios’) definidos com base no máximo da função de verossimilhança (MFV ou MLE, em inglês) que são muito utilizados para avaliar os modelos. Em problemas regulares, a estatística da razão de verossimilhanças (ou “Likelihood Ratio” – LR) converge para a distribuição qui-quadrado com m graus de liberdade, onde m é a diferença entre as dimensões dos espaços paramétricos sob as duas hipóteses testadas (Terra, 2013).

A função de verossimilhança é definida como a função de densidade de probabilidade conjunta dos dados observados, em função dos parâmetros do modelo (ARIMA, no caso, apresentados na descrição da equação do modelo). Os estimadores de máxima verossimilhança são definidos como aqueles valores dos parâmetros, com relação aos dados observados, que são os mais verossímeis (prováveis), e maximizam a função de verossimilhança (MFV).

Existem critérios definidos para avaliar os modelos. De modo geral, quanto menor o “information criteria (IC)”, melhor o modelo, já que são proporcionais ao valor do “log likelihood” e, consequentemente, à variância. Além disso, ambos os critérios penalizam modelos com muitas variáveis. O sinal positivo ou negativo não tem um significado importante, então quanto menor o valor (considerando o sinal), melhor – veja mais nessa discussão do reddit. Dentre os principais critérios baseados no MFV, estão:

* AIC (Critério de Informação de Akaike) – distância relativa esperada entre dois modelos probabilísticos: admite a existência de um modelo “real” (com um alto número de dimensões) que descreve os dados e tenta escolher outro dentre um grupo de modelos avaliados, o que minimiza a distância (ou divergência) de Kullback-Leibler (veja mais no link). Essa distância é uma medida de quanta informação é “perdida” ao tentar representar um conjunto de medidas utilizando uma base conhecida. O AIC é definido por:

Onde Lp é a função de máxima verossimilhança do modelo e p é o número de variáveis explicativas consideradas no modelo.

* AICc – correção da AIC para amostras de tamanho finito, cujo termo somado ao AIC depende do modelo estatístico utilizado. Supondo-se que o modelo é univariado, linear e tem resíduos normalmente distribuídos, a fórmula é:

Onde n indica o tamanho da amostra e k indica o número de parâmetros. O AIC foi desenvolvido sob o conceito de que, assintoticamente (quando o tamanho da amostra tende ao infinito), ele converge para o valor exato da divergência de Kullback-Leibler. No entanto, quando há um número finito de amostras, este estimador se torna polarizado. Com isto, o AIC não pode falhar em escolher um modelo mais parcimonioso, podendo até escolher o modelo de maior ordem entre todos os modelos comparados. Daí surgiu a necessidade da correção.

* BIC (Critério de Informação Bayesiano) – definido como a estatística que maximiza a probabilidade de se identificar o modelo dentre os avaliados, considerando-se a existência de um “modelo verdadeiro” que descreve a relação entre a variável dependente e as diversas variáveis explanatórias dentre os diversos modelos sob seleção. A penalidade devido ao número de termos é maior do que no AIC.

Onde Lp é a função de máxima verossimilhança do modelo e p é o número de variáveis explicativas consideradas no modelo.

O AIC é o melhor para previsão, pois é assintoticamente equivalente à validação cruzada, enquanto que o BIC é melhor para explicação, uma vez que permite uma estimativa consistente do processo de geração de dados subjacente.

A função auto.arima() do R pode estimar modelos através de um algoritmo de ajuste mais eficiente, usando somas condicionais de erros quadráticos, para evitar excesso de tempo computacional para séries longas ou para modelos sazonais complexos. Quando este processo de estimativa está em uso, a função aproxima os critérios de informação para um modelo (porque o “log likelihood” não foi calculado).

A heurística simples é usada para determinar se a estimativa das somas condicionais quadráticas deve ser usada, se o usuário não indicar qual abordagem deve ser usada. Heurística é um método/processo criado com o objetivo de encontrar soluções para um problema muito difícil de se resolver, que envolve a substituição destas questões difíceis por outras de resolução mais fácil a fim de encontrar respostas viáveis, ainda que imperfeitas. Nesse caso, pode surgir o seguinte aviso (warning) em R: “Unable to fit final model using maximum likelihood. AIC value approximated”.

Veja mais sobre Modelo ARIMA e previsão usando o R clicando no link. Nele, é apresentada a utilização de séries temporais auxiliares de regressores/preditores com mais detalhes.

Fontes

• Estatística Básica, Pedro A. Morettin e Wilton de O. Bussab (2004) Ed. Saraiva.
• Time Series Analysis and Applications Using the R Statistical Package, R.H. Shumway & D.S. Stoffer (2016) EZ Edition.
• Modelos para previsão de séries temporais, Morettin & Toloi (1981).
• Apostila de Análise de Séries Temporais, Manoel Ivanildo Silvestre Bezerra (2006) DMEC/ FCT / UNESP.
• Statistical forecasting: notes on regression and time series analysis, Robert Nau, Fuqua School of Business – Duke University.
• Definição de um Modelo de Previsão das Vendas da Rede Varejista Alphabeto, André Furtado Silva (2008) Tese – Universidade Federal de Juiz de Fora, EPD.
• Critérios para seleção de modelos baseados na razão de verossimilhança.
• Modelos Não Lineares Generalizados com Superdispersão, Maria Lídia Coco Terra (2013) Tese – Universidade Federal de Pernambuco, Centro de Ciências Exatas e da Natureza, Departamento de Estatística.
• Análise de Regressão – AIC e BIC.
• Análise dos critérios de informação para seleção de ordem em modelos autorregressivos, Thales E. L. Sobral e Gilmar Barreto (2001) DMCSI/FEEC/UNICAMP.
• Stack Exchange – Interpretação Modelo ARIMA, Interpretação do ARIMA com xreg, Comparação entre BIC e AIC.
• Probability and Statistics in Engineering and Management Science, William W. Hines & Douglas C. Montgomery (1990) – John Wiley & Sons, New York.
• Quora – Which are the best econometrics models (VAR, VEC, ARIMA) for forecasting GDP, Inflation, and stocks?

ps: Diferençar ou diferenciar? As duas palavras existem na língua portuguesa. Significam “distinguir, discriminar” ou também “aplicar cálculo diferencial (calcular as diferenças de uma função ou sequência)”. O verbo “diferençar” é formado a partir de derivação sufixal (quando acrescenta-se um sufixo a uma palavra já existente, alterando o sentido da mesma). Já o verbo diferenciar poderá ter sua origem na palavra em francês différencier.

Posts relacionados:

Tendência e sazonalidade Redes neurais de séries temporais no R Modelo ARIMA e previsão no R Correlação