A transformada de Fourier é comumente usada para converter um sinal no tempo em um espectro de frequência. Esse método utiliza o fato de que toda função não-linear pode ser representada como uma soma de ondas senoidais (infinitas). A transformada separa um sinal de tempo e retorna informações sobre a frequência de todas as ondas senoidais necessárias para simular o sinal de tempo. A imagem exibida no post This Animation will tell you everything about the connection between time and frequency domain of a signal realmente cumpre o que o título promete.
Séries de Fourier
Segundo o matemático francês Joseph Fourier (1768-1830), qualquer sinal periódico pode ser decomposto em uma soma de ondas senoidais puras. Nelas, a frequência de cada senoide é um múltiplo inteiro da frequência fundamental da onda distorcida, denominados “harmônicos”. O sinal x(t) pode ser expresso como a série trigonométrica de Fourier:
\(x(t)=\frac{a_0}{2}+\sum\limits_{k=1}^{\infty}\left[a_k\cdot cos\left(\frac{2\pi}{T}\cdot kt\right)+b_k\cdot sen\left(\frac{2\pi}{T}\cdot kt\right)\right]\) (eq. 1)
sendo:
\(a_k=\frac{2}{T}\int_T x(t)\cdot cos\left(\frac{2\pi}{T}\cdot kt\right)dt\), k=0,1,2,… (eq. 2)
\(b_k=\frac{2}{T}\int_T x(t)\cdot sen\left(\frac{2\pi}{T}\cdot kt\right)dt\), k=1,2,… (eq. 3)
onde:
\(T=\frac{2\pi}{\omega_0}\) é o período fundamental do sinal x(t) – período de todas as amostras colhidas, ou seja, o tempo entre a primeira amostra e a última. As integrais acima são tomadas ao longo do intervalo do período T.
Note que somente existe k = 0 na série ak, o que torna a0 (calculado a partir da equação 2) de certa forma representando um valor médio do sinal x(t) no intervalo de um período T.
A equação 1 é conhecida como “equação de síntese” e as equações 2 e 3 são conhecidas como “equações de análise” (ou também coeficientes) da série trigonométrica de Fourier, que recebe esse nome por apresentar termos com senos e co-senos. Existe também a série exponencial (ou complexa) de Fourier, aplicada quando o sinal periódico contínuo tem valores complexos, com parte real e parte imaginária. Nesse caso, o sinal pode ser escrito como:
\(x(t)=\sum\limits_{k=-\infty}^{\infty}c_k\cdot e^{i{\cdot\frac{2\pi}{T}\cdot kt}}\) (eq. 4)
sendo:
\(c_k=\frac{1}{T}\int_T x(t)\cdot e^{-i{\cdot\frac{2\pi}{T}\cdot kt}}dt\), k=0,\(\pm\)1,\(\pm\)2,… (eq. 5)
Enquanto que a série de Fourier é usada para representar uma função periódica por uma soma discreta de exponenciais complexas (ou senos e cossenos), a transformada de Fourier é usada para representar uma função geral (não necessariamente periódica) por uma superposição contínua ou integral de exponenciais complexos. Dessa forma, a série pode ser representada no domínio das frequências.
Transformada de Fourier
Para sequências de valores uniformemente espaçados, a Transformada Discreta de Fourier (“Discrete Fourier Transform” – DFT) é definida como:
\(X_k = \sum\limits_{n=1}^{N-1}x_n e^{-i{\cdot\frac{2\pi}{N}\cdot kn}}\) (eq. 6)
Onde:
- N = número de amostras
- n = n-ésima amostra (ordem do harmônico)
- k = frequência atual (0 Hz a N-1 Hz)
- Xk = números complexos resultantes da DFT (amplitude e fase)
- xn = números complexos (com parte imaginária nula ou não) do valor do sinal no instante n
A ordem do harmônico representa o número de vezes que a frequência desse harmônico é maior que o componente básico.
O algoritmo Transformada Rápida de Fourier (“Fast Fourier Transform” – FFT), que divide recursivamente o DFT em DFT menores, diminuindo drasticamente o tempo de computação necessário.
Veja esse exemplo (adaptado de Ritchie Vink – Understanding the Fourier Transform by example) de um sinal simples no tempo, contendo uma adição de duas ondas senoidais (uma com frequência de 40 Hz e outra de 90 Hz, com metade da amplitude da primeira):
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(0, 0.5, 500) # 500 números, de 0 a 0.5 -> 1 kHz de amostragem
s = np.sin(40 * 2 * np.pi * t) + 0.5 * np.sin(90 * 2 * np.pi * t)
plt.ylabel("Amplitude")
plt.xlabel("Tempo (s)")
plt.plot(t, s)
plt.savefig('fft_ts.png')
plt.close()

Para calcular um espectro da frequência do sinal de tempo mencionado acima, é feita uma FFT nessa sequência (disponível na biblioteca numpy – fft).
A saída é formada pelas amplitudes complexas dos exponenciais complexos que representam seu sinal, ordenados pela frequência. Se compararmos o primeiro valor da sequência (índice 0) com o último valor da sequência (índice 499), podemos ver que as partes reais de ambos os números são iguais e que o valor dos números imaginários também é igual em magnitude, diferindo apenas no sinal. Ou seja, os números são complexos conjugados uns dos outros, o que é verdade para todos os números na sequência. Assim, como a segunda metade da sequência não nos fornece novas informações, precisamos somente metade da sequência da FFT.
Cada saída numérica discreta da FFT corresponde a uma determinada frequência. A amplitude de uma certa frequência da onda é calculada tomando o valor absoluto do número, e a fase é obtida calculando o ângulo desse número.
Usando a série definida anteriormente e aplicando a função FFT, pode-se criar um gráfico das amplitudes em função das frequências. Para isso, deve-se calcular um vetor com as respectivas frequências (1/T, onde T é o período), sendo que o período é definido pela diferença entre dois instantes. O exemplo a seguir também seleciona a primeira metade da sequência e normaliza as amplitudes pelo número de amostras (divide por N):
fft = np.fft.fft(s)
T = t[1] - t[0] # 0.001 -> 1/T = 1000
N = s.size
#f = np.linspace(0, 1 / T, N)
# fornece os componentes de frequência correspondentes aos dados
f = np.fft.fftfreq(len(s), T)
frequencias = f[:N // 2]
amplitudes = np.abs(fft)[:N // 2] * 1 / N
plt.ylabel("Amplitude")
plt.xlabel("Frequência (Hz)")
plt.bar(frequencias, amplitudes, width=1.5)
plt.savefig('fft_freq.png')
plt.close()
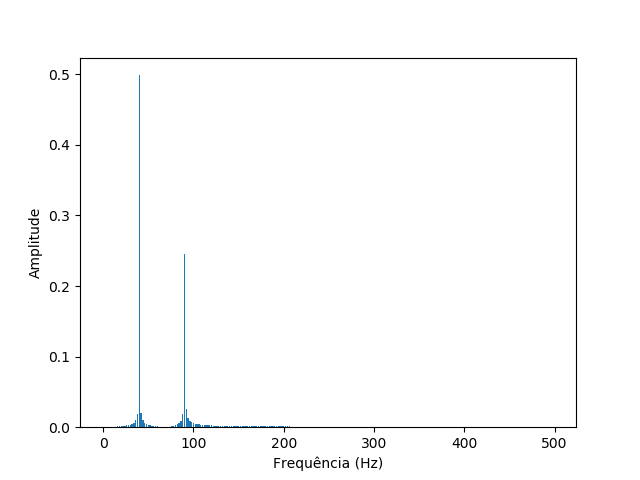
Assim, o primeiro gráfico apresenta as informações da amplitude em função do tempo, enquanto que o segundo, em função das frequências. Para manter informações sobre tempo e frequências de um espectro, precisamos fazer um espectrograma: tempo no eixo x, frequência no eixo y e amplitude na escala de cores.
O método “spectrogram” (do pacote scipy) recebe um vetor com a série temporal e retorna um vetor de frequências, um vetor de tempos segmentados e o espectrograma do sinal. O método “pcolormesh” (do pacote matplotlib) cria o gráfico de cores com uma grade retangular não regular.
O mesmo resultado pode ser obtido pelo método “specgram” do pacote matplotlib. Nesse método, o parâmetro “Fs” indica a frequência de amostragem (amostras por unidade de tempo), “NFFT” é o número de pontos de dados usados em cada bloco para a FFT e “scale_by_freq” especifica se os valores de densidade resultantes devem ser redimensionados pela frequência de redimensionamento, que fornece densidade em unidades de Hz-1 (está falso porque a frequência de amostragem informada é de 1kHz).
plt.specgram(s, NFFT=N-1, Fs=1/T, scale='linear', scale_by_freq=False)
plt.colorbar()
plt.ylabel('Frequência (Hz)')
plt.xlabel('Tempo (s)')
plt.savefig('fft_spectrogram.png')
plt.close()

Note que os picos do gráfico de frequência (~0.5 em 40 Hz e ~0.25 em 90 Hz) estão representados no espectrograma, com a maior parte das frequências iguais a zero (roxo).
Fontes
- J. A. M. Felippe de Souza – Séries de Fourier
- Wikipedia – Discret Fourier transform


2 comments