Quando contamos com um grande número de observações, pode ser de interesse criar grupos, onde os são semelhantes entre si e diferentes dos que estão em outros grupos. A análise de agrupamento (cluster) é uma técnica estatística usado com essa finalidade.
Nessa análise, pode ser aplicado um método hierárquico (com um algoritmo capaz de fornecer mais de um tipo de partição dos dados) ou não-hierárquico (deve-se fornecer uma partição inicial). Dentre os métodos hierárquicos, existem os aglomerativos (os elementos começam separados e vão sendo agrupados em etapas) ou divisivos (cluster inicial é quebrado em outros menores), para então escolhermos o número ideal de clusters.
Para definir a semelhança (ou diferença) entre os elementos, é usada uma função de distância. Geralmente, essa função é a distância euclidiana: o somatório das diferenças ao quadrado entre a característica de dois elementos. Quanto mais próximo de zero for a distância euclidiana, mais similares são os objetos comparados. Existem também outras distâncias usadas, como a Manhattan e a Minkowski.
No caso de uma análise bi-dimensional, pode acontecer de uma das variáveis estar em uma ordem de grandeza diferente da outra. Assim, é importante fazer a normalização (por exemplo, dividir a série toda pelo seu máximo, para que todos os valores fiquem entre zero e um) para que ambas tenham valores compatíveis entre si.
Aglomeração hierárquica
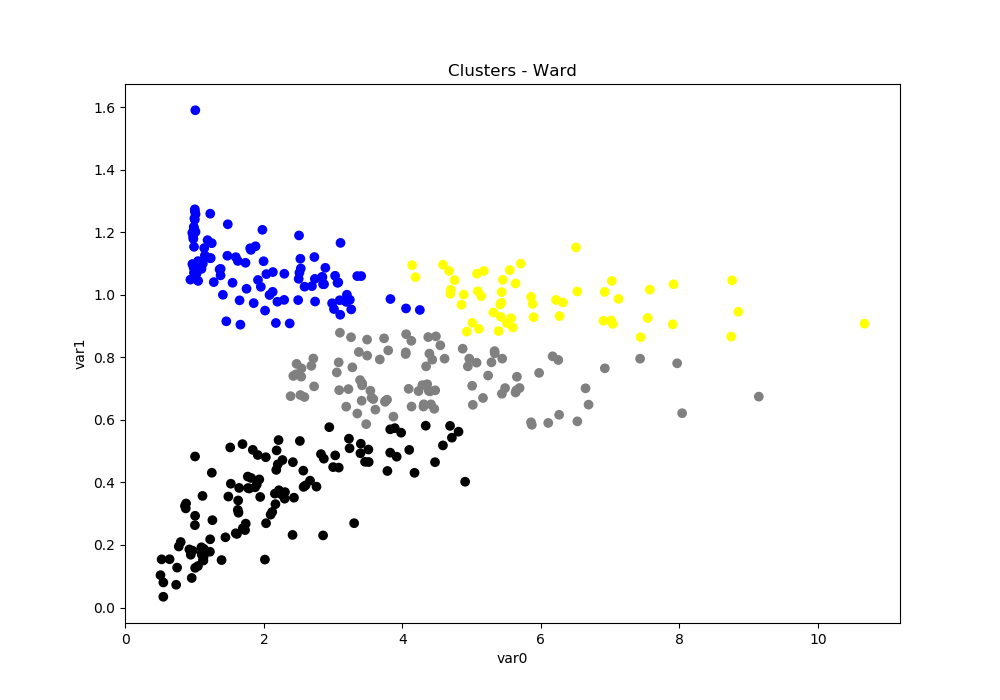
O método de Ward usa aglomeração hierárquica, calculada como a soma de quadrados entre os dois agrupamentos feita sobre todas as variáveis. Em cada estágio, combinam-se os dois agrupamentos que apresentarem menor aumento na soma global de quadrados dentro dos agrupamentos.
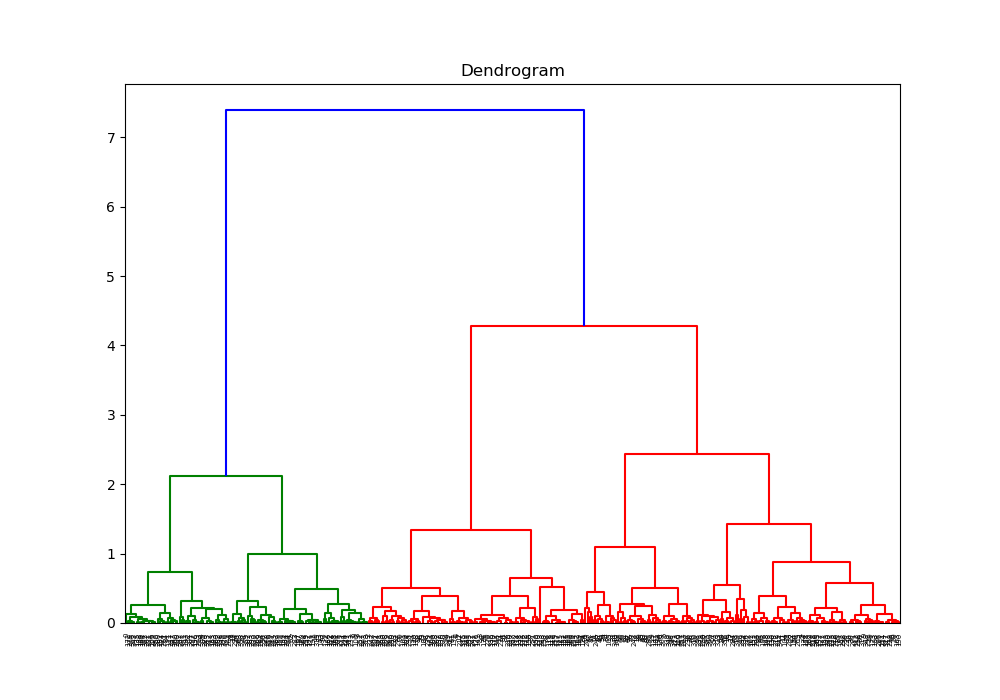
O dendrograma (dendro = árvore) é um diagrama de árvore que exibe os grupos formados por agrupamento de observações em cada passo e em seus níveis de similaridade. De modo geral, um bom ponto de decisão da clusterização final é onde os valores de distância mudam consideravelmente, ou seja, a distância vertical mais alta que não cruza com os clusters (sem linhas horizontais). Existem pacotes em algumas linguagens de programação que fazem os dendrogramas e pintam com cores diferentes cada um dos grupos, definidos conforme esse critério.
Aglomeração não-hierárquica
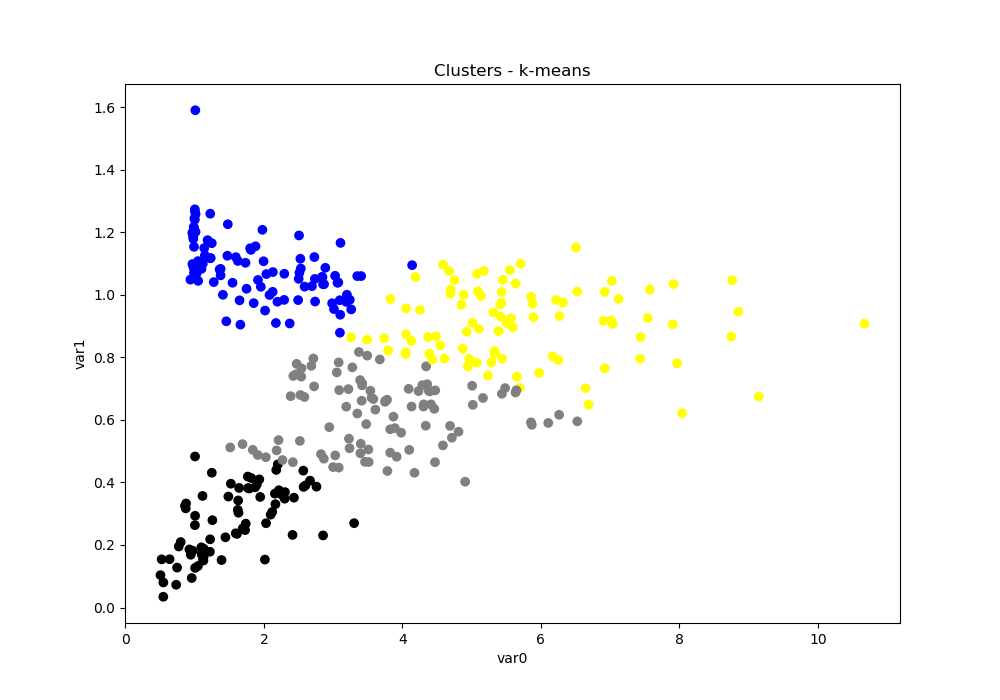
O método k-médias (k-means) é um exemplo de método não-hierárquico com aprendizado não-supervisionado para definir os elementos de um número K de clusters. Costuma ser usado quando se têm muitos objetos para agrupar, com pequenas variações, por ser mais preciso. Não confundir com o K-nn (K-nearest neighbors), que usa aprendizado supervisionado para um número K de vizinhos que têm voto na determinação da posição de um novo elemento.
O critério mais utilizado de homogeneidade dentro do grupo e heterogeneidade entre os grupos é o da soma dos erros quadráticos baseado na Análise de Variância – quanto menor for este valor, mais homogêneos são os elementos dentro de cada grupo e melhor será a partição. Os centroides (ponto em que as coordenadas são as médias das coordenadas dos pontos que formam uma figura geométrica) são dispostos aleatoriamente para inicialização, cuja posição é recalculada a cada iteração (recálculo da distância entre cada objeto e centroide).
Como esse método necessita de um número inicial de clusters, pode-se executar o algoritmo para vários quantidades diferentes de clusters e dizer qual dessas quantidades é o número ótimo. O ideal é que a distância das observações até o centro do agrupamento que ela pertence tenda a zero, ou seja, a soma dos quadrados intra-clusters (ou do inglês within-clusters sum-of-squares, comumente abreviado para wcss) deve ser a menor possível. Esse procedimento é chamado de “método do cotovelo”, devido ao formado do gráfico gerado de wcss versus número de clusters. O wcss é uma métrica que assume que seus clusters são convexos e isotrópicos, ou seja, se os clusters são alongados ou de formato irregular essa é uma métrica ruim.
No gráfico do cotovelo, o ponto que indica o equilíbrio entre maior homogeneidade dentro do cluster e a maior diferença entre clusters, é o ponto da curva mais distante de uma reta traçada entre os pontos inicial e final.
Implementação em python
A biblioteca “SciPy” permite calcular e plotar o dendrograma de duas séries de dados – no caso do script de exemplo, duas colunas de uma data frame. Observando-se a figura, é possível obter o melhor número de grupos em que a amostra deve ser dividida. Esse valor deve ser usado na classe “AgglomerativeClustering” da biblioteca “scikit-learn” (chamada como “sklearn”) para agrupar esses dados nesse número de clusters. Nos dois procedimentos, foi utilizado o método de ward (parâmetro “linkage”). Por fim, pode-se plotar um gráfico de uma variável em função da outra, com um mapa de cores para diferenciar cada cluster.
A biblioteca “scikit-learn” possui implementado o método “k_means“. Como ele recebe de entrada um numpy.array, o atributo “values” de um pandas.DataFrame retorna seus valores em tal formato. No algoritmo, ‘n_clusters’ indica o numero de grupos buscados, ‘init’ indica o tipo de inicialização e ‘n_init’ indica a quantidade de vezes que o algoritmo será executado. Quanto ao tipo de inicialização, ela pode ser uma forma otimizada (‘k-means++’, padrão), randômica (‘random’) ou receber um ndarray com as posições iniciais de cada cluster – nos códigos, é usada a última opção.
Dentre todas as ‘n_init’ execuções, é retornada aquela com o menor valor de erro quadrático. O método retorna três valores: um um numpy.array com k linhas e m colunas contendo os centroides finais; um numpy.array contendo os rótulos de cada objeto; o valor de erro quadrático da solução retornada.
Quanto ao método do cotovelo, o wcss calculado recebe o nome de ‘inertia’ na classe “KMeans”. O melhor número de agrupamentos usa os “wcss” calculados e seus respectivos números de grupo para calcular o número ótimo. Esse valor é impresso na tela, mas pode retornar na função e ser usado como argumento na função de cálculo de cluster – no início do script principal, a número de clusters é fixado em 4.
Assim, o código compartilhado no Github (vinioger/cluster) está organizado a partir do script principal (cluster.py) que carrega um arquivo CSV com dados de exemplo (example.csv) e importa outro arquivo com as funções a serem utilizadas (functions.py):
- ward_dendrogram(data): calcula e imprime o dendrograma (as cores indicam quantos grupos o algoritmo sugere que devem existir)
- ward_cluster(data, n_clusters, maximum): calcula e imprime o gráfico da variável var1 em função da var0 (já “desnormalizada”) com os grupos identificados em escala de cores
- kmeans_elbow(data): calcula o número ótimo de clusters segundo o método do cotovelo
- kmeans_cluster(data, n_clusters, maximum): calcula e imprime o gráfico das variáveis com escala de cores
A função “sanitize” normaliza uma das colunas e monta o numpy.array “data” com as duas variáveis. A função “colormap” permite ter mais controle para definir qual cor deve estar associada com cada número de cluster (e para cada método, de modo a ficarem compatíveis), mas você pode usar uma string que define uma escala já pré-definida – a opção ‘jet’ está comentada, mas você pode ver todas as opções na documentação do matplotlib. Dica: para fenômenos cíclicos, existem os “cyclic colormaps”, em que a cor do maior valor é igual à do menor valor.
Análise comparativa
Se acordo com o dendrograma, são sugeridos somente dois agrupamentos para todos os dados. Já pelo método do cotovelo, é impresso na tela a sugestão de 5 grupos. Nos scripts, foi forçado para ocorrer o agrupamento em 4 clusters. Em um teste com a aglomeração hierárquica, o linkage “average” usa a média das distâncias de cada observação dos dois conjuntos, que resultou em dois grupos principais e outros dois com os respectivos pontos outliers.
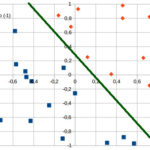
Comparando-se o resultado do método de Ward e o k-means, nota-se que somente alguns pontos das fronteiras entre os grupos é que mudam de grupo, mas o padrão geral é mantido. Uma medida de caracterização dos clusters formados é a soma das diferenças ao quadrado com relação ao centro do cluster, chamado de SSW (“Within sum of squares”). Um SSW menor significa que há menos variação nos dados desse cluster. Na maioria dos casos, o k-means, por ser iterativo, minimizará o SSW um pouco melhor do que Ward. Por outro lado, Ward está mais apto a “descobrir” aglomerados de formato não tão redondo ou menos semelhante ao que normalmente o k-means encontraria.
Os números de cluster atribuídos (e que aparecem nos gráficos no caso de incluir uma legenda) não têm uma ordem. Se você deseja impor uma ordem ou nomes específicos a eles, você pode rotulá-los novamente como quiser. Veja no post Como ordenar agrupamentos para fazer isso.
Fontes
- Oper – O que é análise de cluster?
- Seidel et al (2008) – Comparação entre o método Ward e o método K-médias no agrupamento de produtores de leite
- Stack Abuse – Hierarchical Clustering with Python and Scikit-Learn
- Pizza de Dados – Como definir o número de clusters para o seu KMeans
- Mineração de Dados em Python – Análise de agrupamento de dados



2 comments