Muitas variáveis podem ser tratadas como um sinal, que é a evolução de uma grandeza ao longo do tempo tempo (ou do espaço), em um determinado ponto. Um dos exemplos mais clássicos é a do sinal elétrico, que geralmente é a variação da corrente ou da tensão em função do tempo. Dentre alguns problemas que atingem a rede elétrica estão: sobretensões, quedas de tensão, variações de frequência, flutuações de tensão (cintilação), ruído e distorção harmônica. Uma distorção pode ser do tipo linear (de amplitude ou de fase) ou não-linear, esta gerada principalmente por motores e lâmpadas fluorescentes conectadas à rede.
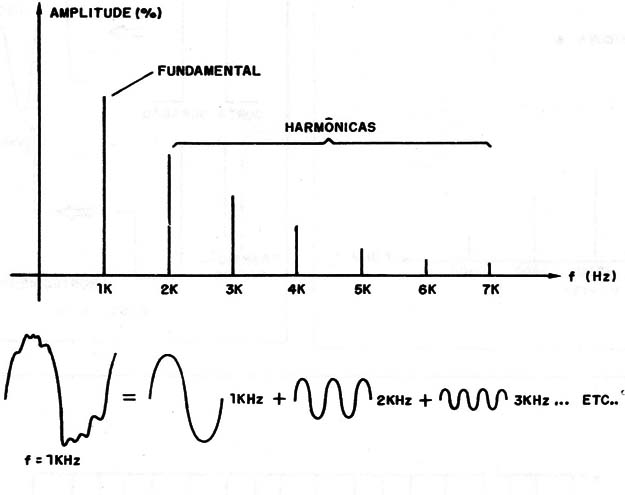
Em um sinal periódico decomposto em uma soma de ondas senoidais puras, são denominados “harmônicos” cada senoide associado a uma frequência cujo valor é um múltiplo inteiro da frequência fundamental (primeiro harmônico) da onda distorcida (veja mais no post sobre Séries e Transformada de Fourier). Uma das formas de detectar a distorção de um sinal elétrico é estimulando um dispositivo de teste com uma onda senoidal pura e realizar uma análise espectral da saída. Um dos resultados da não linearidade de um amplificador é a distorção harmônica.
A amplitude de uma variável periódica é uma medida de sua mudança em um único período (como tempo ou período espacial). A amplitude do quadrado médio da raiz (RMS, do inglês “Root Mean Square”) é definida como a raiz quadrada da média ao longo do tempo do quadrado da distância vertical do gráfico do estado de repouso.
Existem várias medidas comumente usadas para indicar a distorção harmônica de uma forma de onda com um único número. Quando o principal critério de desempenho é a “pureza” da onda senoidal original (em outras palavras, a contribuição da frequência original em relação aos seus harmônicos), a medição é mais comumente definida como a razão da amplitude RMS de um conjunto de frequências harmônicas mais altas à amplitude RMS da primeira frequência harmônica (ou fundamental).
Assim, a distorção harmônica total é a composição das distorções harmônicas individuais que expressa o grau de desvio da onda em relação ao padrão ideal, normalmente referenciada ao valor da componente fundamental. Duas expressões matemáticas de THD são geralmente utilizadas:
\(THD_F=\frac{\sqrt{\sum\limits_{n=2}^{N}h_n^{2}}}{h_1}=\frac{\sqrt{h_1^{2}+h_2^{2}+…+h_N^{2}}}{h_1}\) (“fundamental”)
\(THD_R=\frac{\sqrt{\sum\limits_{n=2}^{N}h_n^{2}}}{\sqrt{\sum\limits_{n=1}^{N}h_n^{2}}}=\frac{\sqrt{h_2^{2}+h_3^{2}+…+h_N^{2}}}{\sqrt{h_1^{2}+h_2^{2}+h_3^{2}+…+h_N^{2}}}\) (“RMS”)
Onde xn são as amplitudes dos harmônicos de ordem n. Os valores dos índices podem ser multiplicados por 100% para serem porcentuais ou calculados seus logaritmos para serem expressos em dB.
Em baixos níveis de distorção, a diferença entre os dois métodos de cálculo é insignificante. Por exemplo, um sinal com THDF de 10% tem um THDR muito semelhante de 9,95%. No entanto, em níveis mais altos de distorção, a discrepância se torna grande. Por exemplo, um sinal com THDF 266% tem um THDR de 94%.
Ainda existe a THD+N, que é a distorção harmônica total mais ruído (do inglês “noise”). É o mesmo cálculo do THDF, mas o ruído é incluído no numerador, o que permite melhor comparações entre dispositivos. Veja mais informações no post THD and THD+N – Similar, but not the same.
Nos sistemas de energia, um menor THD significa redução no pico de correntes, aquecimento, emissões e perda de núcleo nos motores. Nos sistemas de áudio, uma menor distorção significa que os componentes de um alto-falante, amplificador ou microfone ou outro equipamento produzem uma reprodução mais precisa de uma gravação de áudio. Nas radiocomunicações, um THD menor significa emissão pura de sinal sem causar interferências em outros dispositivos eletrônicos.
Uma outra definição de THD é usada em Czekalski (2012), semelhante à THDR:
\(THD_C=\frac{\sqrt{\sum\limits_{n=3}^{N}h_n^{2}}}{\sqrt{h_0+\sum\limits_{n=1}^{N}h_n^{2}}}=\frac{\sqrt{h_3^{2}+h_4^{2}+…+h_N^{2}}}{\sqrt{h_0+h_1^{2}+h_2^{2}+h_3^{2}+…+h_N^{2}}}\) (“Czekalski”)
Como diferenças (no interior das raízes), estão a remoção do 2° harmônico no numerador e a inclusão da componente constante da série de Fourier no numerador (ela só será ausente se a ordenada média da função for igual a zero durante todo o período). Geralmente, o termo constante \(a_0\) é igual à média da função tomada sobre um ciclo completo.
Cálculo dos harmônicos usando séries de Fourier
Considerando-se a forma geral da série trigonométrica de Fourier, são calculados os coeficientes ak e bk para o cálculo de y(t) dos k harmonicos. Considera-se T o período fundamental do sinal x(t) – caso o sinal tenha período igual ao comprimento da própria série, esse será o período fundamental.
Esse cálculo é realizado para cada um dos harmônicos informados em uma lista – no caso, essa lista abrange um intervalo de 1 até o número de amostras do sinal. Para cada harmônico, é calculado o valor de ak, bk e y(t) – nesse caso, somando a média dos valores do sinal de entrada ao vetor de somatórios ak e bk. Desse modo, é criada uma lista de vetores numpy contendo os valores de y(t).
Para calcular a amplitude dos harmônicos, foi feita a diferença do máximo e do mínimo valor de y(t) e dividido por dois.
Cálculo dos harmônicos usando transformada de Fourier
Considerando-se que a amostragem no tempo é uniforme, faz-se uso da transformada rápida de Fourier (FFT) implementada no pacote numpy (usa a série exponencial/complexa de Fourier). Cada saída numérica discreta da FFT corresponde a uma determinada frequência. A amplitude de uma certa frequência da onda é calculada tomando o valor absoluto do número usando-se o método numpy.abs – para um número complexo “a + ib”, o valor absoluto é “sqrt(a²+b²)”.
Calculando THD no python
Do vetor resultante de algum dos métodos anteriores, são selecionados os harmônicos necessários para o cálculo de THD conforme alguma das três definições apresentadas. Para um determinado sinal, pode-se aplicar os cálculos de THDF, THDR e THDC usando os harmônicos calculados usando série de Fourier ou transformada de Fourier (seis combinações) e comparar os resultados. Ainda pensando em THDC, pode-se explorar o impacto das diferenças impostas no comportamento do índice.
Fontes
- Baptista, José M. R. e colab. Voltage Wave Quality in Low Voltage Power Systems. Renewable Energy and Power Quality Journal, v. 1, n. 1, p. 117–122, Abr 2003. Disponível em: http://dx.doi.org/10.24084/repqj01.317.
- On the definition of total harmonic distortion and its effect on measurement interpretation. IEEE Transactions on Power Delivery, v. 20, n. 1, p. 526–528, Jan 2005. Disponível em: http://dx.doi.org/10.1109/TPWRD.2004.839744.
- Wikipedia – Total harmonic distortion. Disponível em: https://en.wikipedia.org/wiki/Total_harmonic_distortion
- Czekalski, D., Chochowski, A., & Obstawski, P. (2012). Parametrization of daily solar irradiance variability. Renewable and Sustainable Energy Reviews, 2461-2467. Disponível em: https://doi.org/10.1016/j.rser.2012.01.069.