Fluidos geofísicos e Meteorologia

O texto e os slides a seguir fazem parte de um seminário sobre fluidos geofísicos em Meteorologia apresentado na disciplina de Mecânica dos Fluidos do Instituto de Física da USP. Nesse trabalho, é realizada uma caracterização da atmosfera como um fluido, apresentação das equações fundamentais, forças envolvidas, escalas e alguns conceitos básicos em meteorologia dinâmica sinótica com aplicações. O intuito é apresentar esses tópicos como motivação para estudos mais aprofundados posteriormente. (link para arquivo)

Introdução

Meteorologia é a ciência que estuda a atmosfera e seus fenômenos. O ar da atmosfera pode ser considerado como um fluido, pois é uma substância que se deforma continuamente sob a aplicação de uma tensão de cisalhamento (tangencial), cuja força interna que se opõe a sua deformação é denominada viscosidade e está ligada a um processo irreversível de dissipação de energia.

1. Leis e forças

Os movimentos atmosféricos se dão baseadas em determinadas leis:

1) Lei da conservação da massa: massa não pode ser criada nem destruída:

\({\frac{\mathit{d\rho }}{{\text{dt}}}+\rho \vec{{\nabla }}\vec{{v}}=0}\) (1.1)

2) 1ª Lei da Termodinâmica: energia interna é alterada através da realização de trabalho e adição/remoção de calor. O termo adiabático é devido à compressão/expansão e o termo diabático está relacionado com a troca de calor por radiação, mudança de fase, condução molecular e fricção (α=1/ρ é volume específico):

\({\frac{{\text{dT}}}{{\text{dt}}}=\frac{1}{c_{{p}}}\frac{{\text{dQ}}}{{\text{dt}}}+\frac{\alpha}{c_{{p}}}\frac{{\text{dp}}}{{\text{dt}}}}\) (1.2)

3) 2ª Lei de movimento de Newton: movimento só pode ser alterado sob ação de forças, no caso, a soma das forças de gradiente de pressão (1º termo), gravitacional (2º termo) e dissipativas (3º termo):

\({\frac{d\vec{{v}}}{{\text{dt}}}=\sum {\vec{{F}}}_{{i}}=-{\frac{1}{\rho }}\vec{{\nabla }}p+\vec{{G}}+{\vec{{F}}}_{{r}}}\) (1.3)

Forças que provocam e modificam os movimentos da circulação atmosférica:

A principal origem dos movimentos de ar (ventos) é o aquecimento diferencial da superfície terrestre, onde há conversão de energia térmica em cinética por parte das parcelas de ar. A parcela de ar se constitui de um volume que transporta suas propriedades (energia, massa, pressão, temperatura… que se dispõe homogeneamente dentro da parcela) ao longo do tempo e espaço, onde a interação molecular só é importante a poucos centímetros da superfície (por ser um gás, as forças intermoleculares são muito fracas, o que para muitos sistemas é uma boa aproximação). Também possui por característica ser isolada termicamente e adiabática, sua pressão é sempre igual a do meio exterior e sua velocidade é pequena em relação ao ar exterior (certas vezes, essas características não são boas aproximações).

a) Força de gradiente de pressão

Resultado da variação de pressão, direcionando, acelerando ou desacelerando os ventos, embora sua existência independa deles.

b) Forças dissipativas (atrito ou viscosidade)

A fricção age na fronteira do fluido e tende a opor-se ao movimento ou agir no próprio fluido tornando o movimento mais uniforme. A força de viscosidade é resultado das trocas de momento entre as moléculas do fluido para movimentos laminares.

Um fluido newtoniano possui viscosidade constante a uma dada temperatura e pressão conforme a lei de viscosidade de Newton, que descreve a força atuante sobre uma superfície que delimita o elemento de fluido. Normalmente é expressa como a razão de elementos infinitesimais de força e área, sendo denominada tensão (expressão 1.4). Definindo a velocidade como sendo v = uî + vj + wk, temos a Lei de viscosidade de Newton para o sistema de referência representado na figura 1:

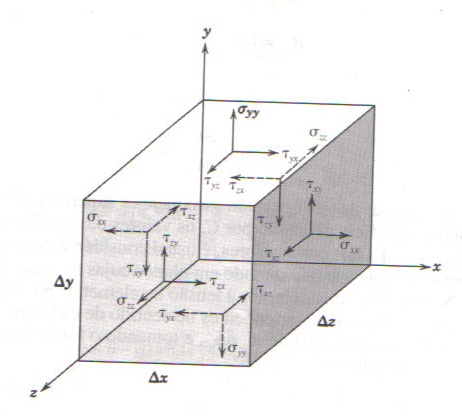
\({\tau _{{{\text{yx}}}}=\mu \frac{{\text{du}}}{{\text{dy}}}}\) (1.4)

Para gases, o coeficiente de viscosidade aumenta com a temperatura, pois as forças coesivas intermoleculares são fracas e a transferência de momento predomina no valor do coeficiente, e um aumento de temperatura implica no aumento da atividade molecular do gás e o aumento do valor do coeficiente. O valor típico do coeficiente de viscosidade do ar é de 1,8.10-5Kg/ms.

Um fluido ideal é idealizado, sendo incompressível e não viscoso. Sob a aplicação de pressão, todos os fluidos são de certa maneira compressíveis. Ao considerar-se uma situação de viscosidade nula, o movimento do fluido se aproxima de fluidos reais onde o gradiente de velocidade e, consequentemente, as tensões de cisalhamento são desprezíveis.

c) Força da gravidade

Atração mútua que os corpos materiais exercem uns sobre os outros.

Como as parcelas de ar não estão em um referencial inercial (planeta Terra), isso implica no aparecimento de uma “força fictícia”, que é a força de Coriolis.

2. Escalas

Uma análise da escala envolvida é uma técnica conveniente para estimar a magnitude espaço-temporal dos fenômenos e dos vários termos das equações que descrevem os movimentos da atmosfera e assim simplificar as equações. Isso é importante para análise das aproximações que serão realizadas. Por exemplo, em microescala, cujos fenômenos tem dimensões espaciais de 1m a 1km e duração da ordem de 1s a 1h, são estudados os processos de formação de gotas, dispersão de poluentes e interação solo-plantas-atmosfera.

As trocas de calor e umidade entre solo e os primeiros metros mais baixos da atmosfera geram turbulências que não podem ser desprezadas quando analisadas nessa escala. Ludwig Prandtl mostrou que muitos escoamentos viscosos podem ser analisados dividindo-se o fluxo em duas regiões, uma delgada próxima à fronteira sólida (a camada-limite) e a outra cobrindo o restante. Na região fora da camada-limite, o efeito da viscosidade é desprezível e o fluido pode ser tratado como não-viscoso.

A camada limite planetária (CLP) é a camada atmosférica em contato com a superfície, com espessura variando de centenas de metros a poucos quilômetros, onde se encontra turbulência tanto de origem mecânica como térmica (convecção), assim como forças de atrito, evaporação, transferência de calor, emissão de poluentes e topografia da superfície. Movimento turbulento pode ser compreendido, de uma forma, como uma condição irregular de fluxo no qual os vários elementos se apresentam variação aleatória no tempo e espaço. Pode ser entendida ainda como o movimento de redemoinhos sobrepostos um ao outro, que chamamos de Vórtices ou Turbilhões (eddies). A CLP também engloba os fenômenos de mesoescala, como tornados, tempestades isoladas, ilhas de calor e brisa marítima.

Em uma análise de grande escala, esses fenômenos não são diretamente considerados. Em escala sinótica e global, o parâmetro de Coriolis começa a ter um efeito maior devido ao tamanho dos fenômenos e deve ser levada em consideração.

Escoamento geofísico:

• a) Sistema de referência em rotação: aceleração da partícula é derivada para um sistema de referências inercial, mas deve-se levar em conta a rotação da Terra (referencial não-inercial).
• b) Turbulência: presente em todas as escalas de movimento nos fluidos geofísicos.

Nos slides da apresentação, existe uma figura com a escala dos fenômenos atmosféricos em área de atuação e tempo de duração, com exemplos deles.

3. Aplicações

No geral, as equações diferenciais parciais que governam os movimentos na atmosfera são extremamente complexas e nenhuma solução geral é conhecida. Para adquirir um entendimento dos movimentos atmosféricos determinantes no tempo e clima é necessário o desenvolvimento de modelos com simplificações sistemáticas das equações fundamentais, que são apropriadas para sistemas atmosféricos específicos e requer cuidado na consideração da escala do movimento envolvido.

3.1 Expressão da taxa de mudança

Considerando uma quantidade escalar ou vetorial arbitrária (T, P, V…) denominada F=F(x,t), podemos calcular sua taxa de mudança em cada ponto seguindo uma partícula de identidade fixa. Assumindo que cada incremento no espaço (dx, dy e dz) associados com campo de velocidades do movimento da partícula temos:

\({\frac{{\text{DF}}}{{\text{Dt}}}=\frac{\partial F}{\partial t}+\left(\vec{{v}}\cdot {\vec{{\nabla }}}\right)F}\) (3.1)

A derivada convectiva (ou advecção, o último termo) representa a mudança no tempo devido ao transporte de uma parcela de fluido de uma local para outro. Em Meteorologia, é comum essa derivada ser expressa da seguinte forma (os termos de u e v compõem a advecção horizontal e w a convecção):

\(\frac{{\text{DF}}}{{\text{Dt}}}=\frac{\partial F}{\partial t}+{u\frac{\partial F}{\partial x}+v\frac{\partial F}{\partial y}}+w\frac{\partial F}{\partial z}\) (3.2)

Para movimentos em escala sinótica, a altura do sistema é muito menor que o raio da Terra e menor que as dimensões nas outras duas dimensões. Além disso, o gradiente horizontal típico é bem menor que o vertical, pois, apesar da variação vertical ser muito grande, w (velocidade vertical) é muito pequena. Portanto, a advecção vertical pode ser desconsiderada em certos casos. Por exemplo, ventos horizontais da ordem de 2 a 10 m/s são geralmente comuns na Camada Limite (o atrito faz com que a velocidade seja menor nas partes inferiores da camada), enquanto o vento médio vertical tem intensidade muito menor, geralmente na ordem de milímetros a centímetros por segundo. Em certos casos não se deve ignorar o gradiente vertical, como por exemplo no estudo de tempestades convectivas. A força do gradiente horizontal de pressão é muito menor que o gradiente vertical de pressão (a variação é cerca de 10 mil vezes menor), mas não há uma força de gravidade horizontal para balancear.

3.2 Equação fundamental do movimento

\(\frac{D\vec{{v}}}{{\text{Dt}}}=-{\frac{1}{\rho }}\vec{{\nabla }}p-\frac{g\vec{{r}}}{r}+\)\(\frac{\mu }{\rho }\left({\vec{{\nabla }}}^{{2}}u\hat{{i}}+{\vec{{\nabla }}}^{{2}}v\hat{{j}}+{\vec{{\nabla }}}^{{2}}w\hat{{k}}\right)\) (3.3)

Caso o termo correspondente à viscosidade seja nulo, temos a equação de Euler para um fluido sem viscosidade em um referencial inercial. Como o planeta Terra é um referencial não-inercial (está em rotação), a equação ganha termos extras na mudança de descrição de referencial: termo devido à mudanças no tempo da velocidade de rotação da Terra (normalmente é desprezado, exceto para modelos paleoclimatológicos), termo da aceleração centrípeta (entra junto com o termo da gravidade, de modo que \({\vec{{g}}={\vec{{g}}}_{{e}}+\vec{{\Omega }}\times \left(\vec{{\Omega }}\times {\vec{{r}}}\right)}\)) e o termo da aceleração de Coriolis (\(2\vec{{\Omega }}\times {\vec{{v}}}_{{r}}\), onde v é a velocidade observada no referencial em rotação e ômega é a velocidade de rotação da Terra).

3.3 Geostrofia

Em coordenadas cartesianas tangenciais, z é paralelo ao vetor radial e aponta para fora, x e y formam um plano tangente à Terra no ponto x0, x aponta para leste e y para o norte, conforme esquema abaixo:

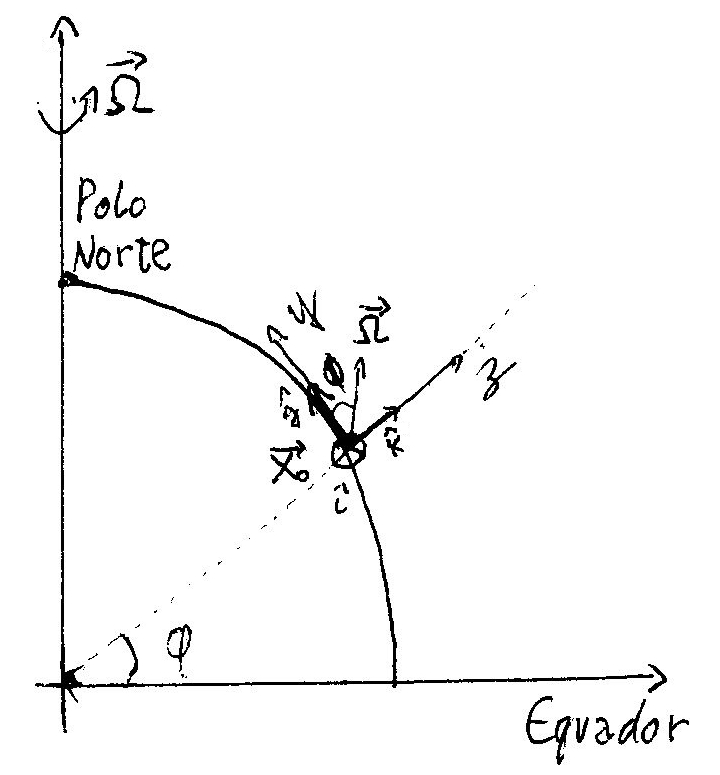
Passando o termo de Coriolis para o novo sistema de coordenadas e definindo \(f=2\Omega {\text{sen}}\varphi\), temos:

\(\frac{D\vec{{v}}}{{\text{Dt}}}=-{\frac{1}{\rho }}\vec{{\nabla }}p-\vec{{g}}+2\Omega w\text{cos}\varphi \hat{{i}}-{\text{fu}\hat{{{j}}}}+2\Omega {\text{sen}}\varphi \hat{k}\) (3.4)

Por análise de escala obtemos a aproximação geostrófica, onde se considera um balanço entre a força de Coriolis e a força do gradiente de pressão para o movimento horizontal, ou seja:

\({\text{fv}}=\frac{1}{\rho }\frac{\partial p}{\partial x}\Rightarrow v\equiv v_{{g}}=\frac{1}{\mathit{\rho f}}\frac{\partial p}{\partial x}\) (Vento geostrófico) (3.5)
\({\text{fu}}=-{\frac{1}{\rho }}\frac{\partial p}{\partial y}\Rightarrow u\equiv u_{{g}}=-{\frac{1}{\mathit{\rho f}}}\frac{\partial p}{\partial y}\) (3.6)

Considerando-se o termo de atrito:

\({\text{fv}}=\frac{1}{\rho }\frac{\partial p}{\partial x}-\mu \frac{\partial ^{{2}}u}{\partial z^{{2}}}\) (3.7)
\({\text{fu}}=\frac{1}{\rho }\frac{\partial p}{\partial y}+\mu \frac{\partial ^{{2}}v}{\partial z^{{2}}}\) (3.8)

Implicando na solução clássica de Ekman na região de fronteira inferior da atmosfera com a CLP. A camada de Ekman possui aproximadamente 2 km de profundidade próximo a superfície, na qual os efeitos do atrito, as forças de Coriolis e gradiente de pressão interagem para produzir um hodógrafo (espiral) de ventos que giram no sentido anti-horário com a altura no Hemisfério Sul. O vento na superfície é nulo e o vento no topo da camada é aproximadamente geostrófico. O transporte líquido do fluido nesta camada é para regiões de baixa pressão.

Sendo as velocidades do vento paralelas às isóbaras em torno dos centros de pressão, com alta pressão a sua esquerda no hemisfério sul, e a sua direita no hemisfério norte. A força de Coriolis e a força do gradiente de pressão atuam em todas as parcelas de ar, sendo o fluxo geostrófico na região exterior à CLP. Vamos ver esse processo em mais detalhes a seguir.

3.4 Coordenadas naturais (vento gradiente, geostrófico e ciclostrófico)

Considerando-se apenas o movimento horizontal descrito pela equação:

\(\frac{D{\vec{{v}}}_{{H}}}{{\text{Dt}}}=\frac{\partial v_{{H}}}{\partial t}+\left(\vec{{v}}\cdot {\vec{{\nabla }}}\right){\vec{{v}}}_{{H}}= \)\(-{\frac{1}{\rho }}-f\hat{{k}}\times {\vec{{v}}}_{{H}}+{\vec{{f}}}_{{{\text{rH}}}}\) (3.9)

Define-se os versores t, n e k, onde:

• t é orientado na direção do escoamento em cada ponto (paralelo à velocidade horizontal em cada ponto);
• n é normal a t, perpendicular ao escoamento e é definido como positivo à esquerda do escoamento;
• k é dirigido verticalmente para cima;

R é o raio de curvatura da trajetória da parcela de ar, sendo R>0 um giro anti-horário e R<0 horário.

Fazendo as devidas substituições, temos que (aceleração é a taxa de mudança da velocidade da parcela de ar somada à aceleração centrípeta devido à curvatura da trajetória):

\(\frac{D\vec{{v}}}{{\text{Dt}}}=t\frac{D\vec{{v}}}{{\text{Dt}}}+\frac{\vec{{n}}}{R}v^{{2}}\) (3.10)

Sendo S(x,y,z) a curva que segue o movimento da parcela de ar no plano horizontal e colocando a força de gradiente de pressão, de fricção e Coriolis, temos, em componentes:

Ao longo do movimento (t):
\(\frac{{\text{Dv}}}{{\text{Dt}}}=-{\frac{1}{\rho }}\frac{\partial p}{\partial S}+f_{{{\text{rt}}}}\) (3.11)

Perpendicular ao movimento (n):
\(\frac{v^{{2}}}{R}=-{\frac{1}{\rho }}\frac{\partial p}{\partial x}-{\text{fv}}+f_{{{\text{rn}}}}\) (3.12)

Casos particulares:

a) Vento gradiente
Escoamento (trajetória da parcela) coincide com as isóbaras \(\left(\frac{\partial p}{\partial S}=0\right)\) e despreza-se a fricção (fr=0 e frn=0). Logo, \(\frac{{\text{Dv}}}{{\text{Dt}}}=0\) e, neste caso, o campo de velocidade é descrito pela equação 3.12 com o termo de fricção nulo. Essa equação representa o balanço do vento gradiente, que pode ser atingido tanto em escoamentos ciclônicos como anti-ciclônicos. Resolvendo a equação para a velocidade, temos que v só é real para:

\(f^{{2}}-\frac{4}{R}\frac{1}{\rho }\frac{\partial p}{\partial n}\gt0\) (3.13)

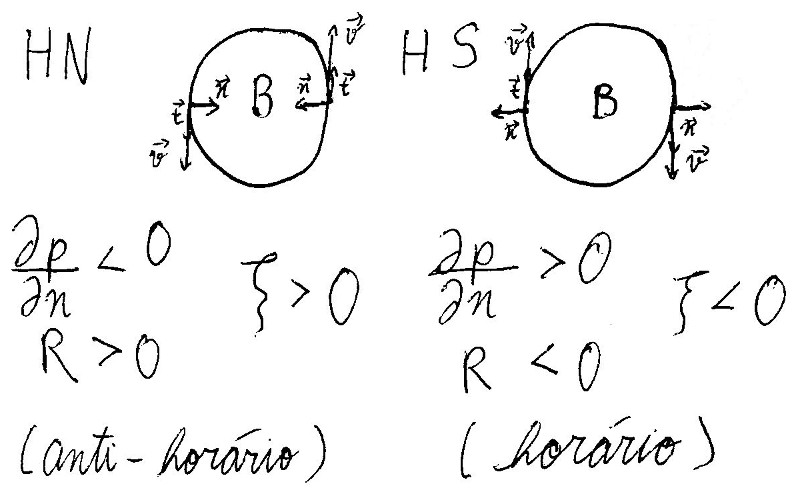
Trajetórias ciclônicas:

Trajetórias anti-ciclônicas:

A aproximação do vento gradiente pode ser utilizada para estimar a pressão central em ciclones em superfície:

\({\overset{{p}}{\underset{{p(n)}}{\int }}{\frac{\partial p}{\partial n}=-\overset{{0}}{\underset{{r}}{\int }}{\mathit{\rho v}\left(f+\frac{v}{R}\right){\text{dr}}}}}\)

\(p(r=0)=p(r)-\overset{{0}}{\underset{{r}}{\int }}{\mathit{\rho v}\left(f+\frac{v}{R}\right)}{\text{dr}}\) (3.14)

b) Vento geostrófico

Ocorre quando R tende a infinito. Essa componente do vento está relacionada à aceleração devida à curvatura da trajetória das parcelas de ar. Esse efeito é mais importante na dinâmica de ciclones pequenos e intensos. Sendo as velocidades do vento paralelas às isóbaras em torno dos centros de pressão, com alta pressão a sua esquerda no hemisfério sul, e a sua direita no hemisfério norte.

c) Vento ciclostrófico

Ocorre quando v²/R >> fv, então temos:
\(\frac{v^{{2}}}{R}=-{\frac{1}{\rho }}\frac{\partial p}{\partial n}\) (3.15)

Para um tornado, temos v ≈ 75m/s e R ≈ 10³m, e temos:
v²/R ≈ (10³ a 104)/10³ = 1 a 10 m/s²
fv ≈ 10-4.10² = 10-2 m/s²
Então, temos que v²/R >> fv.

Nesse balanço, o termo de Coriolis pode ser desprezado, e pode ser encontrado em vórtices ciclônicos com velocidades menores e R pequeno, como os redemoinhos (“dust devil”).

3.5 Vorticidade e circulação

Para definir a taxa de rotação da parcela de fluido, assumiremos que a vorticidade relativa é definida matematicamente como \(\vec{{w}}=\vec{{\nabla }}\times {\vec{{v}}}\), e a parcela é irrotacional quando a vorticidade é nula. A circulação em torno de um círculo fechado C é definida como a integral de linha do componente vetor velocidade tangente à curva C:

\(\Gamma =\underset{{C}}{\oint }{\vec{{v}}d\vec{{s}}=\underset{{s}}{\iint }{\underbrace{\left(\vec{{\nabla }}\times {\vec{{v}}}\right)}_{{=\vec{{w}}}}d\vec{{A}}}}\) (3.16)

Portanto, a circulação em torno de um circuito fechado é igual à integral de superfície da vorticidade, o que pode ser chamado de fluxo de vorticidade. De forma equivalente, temos que a vorticidade em um ponto é igual à circulação por unidade de área:

\(\xi =\frac{\mathit{d\Gamma }}{{\text{dA}}}\) (3.17)

Convenção de sinais:

• Anti-horário => w>0 e Γ>0
• Horário => w<0 e Γ<0

Para movimentos de escala sinótica, que são predominantemente horizontais, o componente vertical (paralelo a k) do vetor velocidade é o mais importante. Assim:

\(\xi =\hat{{k}}\cdot \left(\vec{{\nabla }}\times {\vec{{v}}}\right)=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\) (3.18)

A vorticidade absoluta (vorticidade no referencial inercial) é obtida a partir da seguinte relação de velocidades (velocidade absoluta é a soma da velocidade relativa com a velocidade transferida ao fluido pela rotação):

\(\vec{v}_a=\vec{v}_r+\omega\times r\) => \({\vec{{w}}}_{{a}}=\vec{{w}}+2\vec{{\Omega }}\), onde \(\vec{{\Omega }}=\Omega \text{cos}\varphi \hat{{j}}+\Omega {\text{sen}}\varphi \hat{{k}}\)

Assim, a componente vertical da vorticidade absoluta é definida por \(\vec{{k}}\cdot {\vec{{w}}}_{{a}}=\xi _{{a}}=\xi +f\) (3.19)

3.6 Taxa de mudança da vorticidade absoluta

Conhecendo a vorticidade, assim como sua variação ao longo do tempo, podemos estimar a velocidade vertical w, que é importante na formação de nuvens, perfis verticais de convergência/divergência e dispersão de poluentes. Também pode-se estimar a variação de pressão na superfície assim como crescimento e decaimento dos ciclones de latitudes médias. Para movimentos de grande escala em latitudes médias, os movimentos são quase não-divergentes, ou seja, predomina o componente rotacional do vento. Alguns modelos numéricos atmosféricos (inclusive de previsão de tempo) resolvem as equações completas da vorticidade e divergência ao invés da variação de velocidades horizontais, pois qualquer escoamento pode ser decomposto como a soma de dois vetores velocidade:

• a) Vetor velocidade não-divergente, mas rotacional;
• b) Vetor velocidade divergente, mas irrotacional.

Essas afirmações constituem o Teorema de Helmholtz, e pode ser expresso pela soma da parte rotacional não-divergente e do divergente irrotacional:

\(\vec{v}_H=\vec{v}_\Psi+\vec{v}_\phi\) (3.20)

Partindo das equações para o movimento horizontal (3.9), pode-se deduzir a equação da vorticidade em coordenadas cartesianas:

\(\frac{D}{{\text{Dt}}}\left(\xi+f\right)=\)\(\underbrace{-\left(\xi +f\right){\vec{{\nabla }}}_{{H}}\vec{{v}}}_{a}\)\(-\underbrace{\frac{\partial w}{\partial x}\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\frac{\partial u}{\partial z}}_{{b}}\)\(+\underbrace{\frac{\vec{{k}}}{\rho ^{{2}}}\left(\vec{{\nabla }}\rho \times {\vec{{\nabla }}}p\right)}_{{c}}\)\(+\underbrace{\vec{{k}}\cdot \left(\vec{{\nabla }}\times f_{{r}}\right)}_{{d}}\) (3.21)

Essa é a equação da componente vertical da vorticidade ou também chamada equação da vorticidade, indicando a taxa de mudança de vorticidade absoluta seguindo o movimento de uma parcela de ar.

a) Termo da divergência

Representa a fonte/sumidouro, pode criar/destruir a vorticidade através da convergência/ divergência de massa. Ou seja, a convergência \(\left({\vec{{\nabla }}}_{{H}}\vec{{v}}\lt0\right)\) de massa aumenta a vorticidade ciclônica com o tempo e a divergência \(\left({\vec{{\nabla }}}_{{H}}\vec{{v}}\gt0\right)\) de massa diminui a taxa de rotação da parcela de fluido.

b) Termo de inclinação

Responsável por inclinar os vórtices da direção x,y para a direção vertical. Para que isso ocorra, é necessário que exista um cisalhamento (variação na direção e/ou na velocidade do vento em uma dada distância) vertical do vento horizontal e também que a velocidade vertical w mude na horizontal. Esse termo ajuda a explicar a formação de tornados em tempestades e é importante nas regiões de frontogênese.

Um exemplo numérico representando um “outdraft” à frente de uma tempestade com formação de tornado pode ser visto nos slides da apresentação. Nele, estima-se a vorticidade no centro do tornado. O termo de inclinação produz/destrói a vorticidade através da rotação do cisalhamento vertical do vento horizontal dentro/fora do plano horizontal através dos gradientes horizontais do movimento vertical.

c) Termo solenoide

Não é muito importante no comportamento de sistemas de grande escala.

d) Termo de fricção

Escoamento desacelera mais rapidamente próximo à fronteira, gerando vorticidade. Este mecanismo é responsável pela geração de vorticidade nas asas de aviões e ao longo de construções muito altas.

4. Conclusão

A atmosfera (assim como o oceano, por exemplo) é um fluido geofísico que obedece leis físicas como as de Newton, da termodinâmica, conservação de massa e energia. Os movimentos se estendem desde escalas milimétricas até planetárias, com escalas temporais cobrindo desde segundos até décadas. Esses movimentos podem ser estudados com as mesmas equações da hidrodinâmica e da termodinâmica usadas para qualquer fluido viscoso que obedeçam à hipótese do continuum, ou seja, as variáveis que caracterizam o escoamento são funções contínuas das coordenadas espaciais, desconsiderando a estrutura molecular da matéria.

Uma aplicação que envolve toda essa teoria é no campo de modelagem da atmosfera e previsão do tempo. Os elementos que definem o estado da atmosfera são: pressão, temperatura, umidade, ventos, hidrometeoros (chuva, neve, granizo…), insolação, nebulosidade, visibilidade, etc. Essas são as condições médias que definem o clima e permitem a modelagem da atmosfera em determinadas regiões e também servem de condição inicial para “rodar” um modelo computacional, por exemplo uma previsão de tempo.

5. Referências

• [1] HOLTON, J.R. – An Introduction to Dynamic Meteorology. 2003, 391p.
• [2] WALLACE, J.M. e HOBBS, P.V. – Atmospheric Science: An Introductory Survey. Academic Press, New York, 2006, 467p.
• [3] DUTTON, J.A. – The Ceaseless Wind: An Introduction to the Theory of Atmospheric Motion. 1976, 579p.
• [4] FOX, R.W. e MCDONALD, A.T. – Introdução à Mecânica dos Fluidos. 1992, 662p.
• [5] MARCHETTI, D.H.U. – Notas de Mecânica dos Fluidos (1°sem/2007 – IF/USP)
• [6] ROCHA, R.P. – Notas de aula – Meteorologia Dinâmica I (2°sem/2006 – IAG/USP)

Posts relacionados:

Variações da temperatura no solo Modelo hidrológico SMAP Eventos de divulgação científica Água na atmosfera