A forma com que o calor é transmitido através da terra influencia a temperatura em diferentes níveis de profundidade, ocasionando fatos bem curiosos. Por exemplo, as cavernas possuem temperatura muito estável, independente da profundidade, condições meteorológicas e estação do ano que esteja. Ou também, dependendo da profundidade, podemos ter verão em vez de inverno, em termo de temperatura. Veja como isso é possível através de conhecimentos de Física e trabalho com a equação do calor usando séries de Fourier.

A energia geotérmica é a energia térmica gerada e armazenada no interior da Terra, formada a partir da formação original do planeta (50%) e do decaimento radioativo de elementos como o urânio, o tório e outros minerais (50%). No centro da Terra, as temperaturas podem atingir mais de 5000 °C. A alta temperatura e pressão fazem com que a rocha derreta, criando uma convecção do magma para cima, pois é mais leve que a rocha sólida. As usinas geotérmicas usam o vapor, naturalmente gerado pela água aquecida por essa fonte de calor, para mover turbinas e gerar energia elétrica. Um gêiser se forma devido a reservatórios de água em rochas impermeáveis onde a crosta terrestre é mais fina. A medida que esse volume de água esquenta, ele ganha pressão, aumenta de volume e empurra a coluna d’água para cima (ou simplesmente aquece a água, formando as fontes termais).
Porém, a parte externa da crosta terrestre (onde vivemos) recebe calor principalmente de outra fonte de calor: o Sol. A energia solar é absorvida pelo solo e re-emitida na forma de radiação infravermelha (calor), que será transmitido para a atmosfera e para camadas inferiores do solo. Para esse estudo, desconsidera-se o calor vindo do interior da Terra, o que é uma boa aproximação considerando os primeiro metros de profundidade em regiões cuja crosta tem formação mais antiga e seja mais espessa. Em maiores profundidades, é a energia geotérmica que comanda a temperatura (por isso a maioria das cavernas possuem temperatura muito estável em toda sua extensão).
Equação do calor
Matematicamente, o problema da condução do calor em uma barra semi-infinita atuando como condições de contorno consiste em determinar uma função u(x,t). Considera-se que os parâmetros dependam apenas da profundidade x submetida a uma variação de temperatura periódica f(t) com período T = 2L (que será o dia ou o ano, de acordo com o problema a se estudar). Essa função a ser encontrada deve satisfazer a equação do calor:
\(u_t=Ku_{xx},t\in\mathbb{R},x\gt0\)bem como à condição de fronteira:
\(u(0,t)=f(t),t\in\mathbb{R}\)Para resolver o problema, expressa-se a função temporal f(t) como sua série de Fourier (utilizada aqui em sua forma complexa). Assim, pelo método de separação de variáveis, a solução “chutada” para o problema é:
\(u(x,t)=u(x).f(t)=\sum\limits_{n=-\infty}^{\infty}c_nu_n(x)e^{i2nt\pi/T}\)Substituindo na equação do calor e usando a condição de contorno apresentada, obtém-se o seguinte problema de valor inicial para a determinação de un:
\(u_n”=\frac{2ni\pi}{KT}u_n,x\gt0,u_n(0)=1\)Considerando também que a função un seja limitada em x > 0, temos a seguinte solução para as equações apresentadas:
\(u_n(x)=e^{-(1\underline{+}i)(|n|\pi/KT)^{1/2}x}\)Substituindo-se esta solução encontrada na solução “chutada” e chamando de gama o argumento principal do número complexo cn, finalmente temos:
\(u(x,t)=c_0+2\sum\limits_{n=1}^{\infty}|c_n|e^{-(n\pi/KT)^{1/2}x}cos(\frac{2nt\pi}{T}+\gamma_n-\sqrt{\frac{n\pi}{KT}}x)\)Note que u(x,t) é uma superposição de ondas, correspondendo aos harmônicos de f. Cada onda tem sua amplitude amortecida pelo fator exponencial e cada uma delas está defasada do termo que multiplica x. O amortecimento de cada onda cresce conforme n aumenta, e portanto a primeira onda domina.
Considerando K = 0,002 cm²/s e T 3,15 x 107s (número de segundos em 1 ano), o fator de amortecimento da primeira onda (n = 1) é 0,03 e da segunda onda é de 0,006 a 500 cm. Para x = 445 cm, essa onda está defasada aproximadamente pi e amortecida por um fator de 0,04. Colocando as funções u(x,t) e f(t) para esse valor de x em um gráfico, observa-se que a temperatura do solo em x = 445 cm está completamente defasada da temperatura da superfície. Assim, enquanto a temperatura na superfície é de inverno, em profundidade é verão, e vice-versa. Além disso, a flutuação das temperaturas a essa profundidade é apenas 4% do que acontece na superfície.

Já se considerar T = 86400 s (número de segundos de um dia), temos que a defasagem completa ocorre a 23 cm, e o amortecimento na temperatura se dá por um fator de 0,04. Assim, as variações de temperatura na superfície penetram pouco no solo ao longo do dia, atuando somente na camada mais superficial.
Estudo do ciclo diruno
Segue uma aplicação da variação de calor em função do tempo para diferentes profundidades. Foi elaborado um gráfico a partir da equação apresentada para o primeiro harmônico (n = 1) e período correspondente a 1 dia, onde cada sequência indica os valores de calor transmitido para os diferentes níveis em função do tempo. Também foram construídos gráficos de valores de temperatura do solo obtidos em uma estação meteorológica.

Note que o fluxo de calor é maior quanto mais rasa for a camada do solo na primeira metade do ciclo (manhã e início da tarde). Na segunda metade do dia, o módulo do fluxo de calor ainda é maior próximo da superfície, porém é negativo, indicando perda de calor. Quanto maior a profundidade, menor o módulo do fluxo de calor e maior o atraso em variar esse fluxo.
A estação meteorológica do Instituto de Astronomia, Geofísica e Ciências Atmosféricas (IAG) da USP, localizada no Parque Cientec, está em Latossolo Vermelho-amarelo Argiloso (Struffaldi-de-vuono, Y. 1985) e possui termômetros que medem a temperatura do solo em diferentes níveis de profundidade. São realizadas observações horárias das 7 horas da manhã à meia noite. Veja mais sobre os instrumentos dessa estação meteorológica clicando nesse link.
Foram escolhidos dias do verão e do outono de 2014 sem chuvas no dia anterior (para a água influenciar o mínimo possível no transporte de calor) e com o mínimo de cobertura de nuvens. O comportamento das curvas dos dias observados da mesma estação do ano são basicamente os mesmos, exceto quando da ocorrência de chuvas e/ou nuvens. Assim, seguem os gráficos para os dias 01/02/2014 (verão) e 12/06/2014 (outono), com os valores de temperatura do solo para as profundidades de 0 (superfície), 5, 10, 20, 30 e 40 cm, representados em séries conforme indicadas na legenda, em função do tempo.
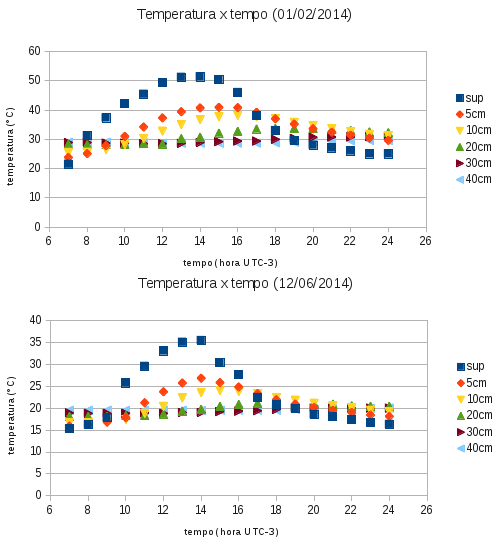
Observando os valores medidos de temperatura, é possível notar o mesmo comportamento descrito teoricamente: quanto mais próximo da superfície, maiores são as variações de temperatura (positivamente na primeira metade do dia e negativamente na segunda metade). A partir das 17 horas, nota-se que a temperatura nos níveis mais profundos é maior do que a da superfície, evidenciando o atraso do fluxo de calor no tempo. Os padrões citados são observadas em ambas as estações, somente diferindo a magnitude das temperaturas atingidas (maiores no verão). A inversão de temperaturas previstas para a profundidade de 445 cm não puderam ser observadas mais próximas da superfície (até 40 cm de profundidade).
Fontes
- Estação Meteorológica do IAG-USP, agradeço pelos dados cedidos e a atenção dada que permitiram esse breve estudo.
- Struffaldi-de-Vuono, Y. 1985. Fitossociologia do estrato arbóreo da floresta da Reserva Biológica do Instituto de Botânica (São Paulo, SP). Tese de doutorado, Universidade de São Paulo, São Paulo.
- Metade do calor da Terra vem do decaimento radioativo
- Trajano, E.: O ambiente subterrâneo: fatores abióticos; 2004; Hipertexto.
- Análise de Fourier e equações diferenciais parciais, Djairo Guedes de Figueiredo, Rio de Janeiro, IMPA, 2005.




Muito boas informações neste relatório consegui utilizar.
Teriam informes sobre as temperaturas desde a superfície até a profundidade de 1 m?
As informações serão usadas na avaliação do teor de cloro agregado em circulação nas redes de distribuição de água potável.
Agradeço.
Eng. Rogério Pinto Muniz
Olá Rogério, que bom que gostou das informações. Nessa estação, a profundida máxima dos termômetros era de 40 cm, então não tinha dados para seções mais profundas de solo. Você pode entrar em contato diretamente com a Estação Meteorológica do IAG-USP e pedir dados das datas que tiver interesse para o seu estudo, lembrando dessa limitação de profundidade.