A energia solar que incide sobre o topo da atmosfera (TOA) interage com uma camada de ar até atingir a superfície terrestre. Os conceitos e cálculos para obter o valor de irradiância no TOA podem ser vistos no post Irradiância solar no topo da atmosfera. A fração do fluxo incidente sobre um sistema que consegue atravessá-lo é chamada de transmitância. Assim, a irradiância que atinge a superfície após interagir com a atmosfera, desconsiderando-se as nuvens, é chamada de irradiância de céu claro (ou CSI, do inglês Clear Sky Irradiance).
A CSI é obtida pelo produto da irradiância no TOA pela transmitância. Mas como definir o seu valor? Existem vários modelos de transferência radiativa que permitem calcular o efeito da atmosfera na propagação da energia solar, obtendo assim a transmitância e a irradiância de céu claro. Alguns deles são mais simplificados, enquanto outros consideram fenômenos que devem ser considerados ou que podem ser negligenciados, conforme a escala de trabalho.
Considerando-se a energia solar total (integrada em todo o espectro de frequências), o método paramétrico permite calcular a energia radiante usando parâmetros atmosféricos especificados. Assim, é calculada a transmitância devido a cada constituinte atmosférico, cuja transmitância total é o produto de todas as transmitâncias parciais.
Modelo C -Iqbal
Dentre os vários modelos paramétricos disponíveis na literatura, Iqbal (1983) apresentou três modelos, denominados A, B e C. De acordo com suas análises, o modelo C é o mais acurado, apesar de não ficar muito distante dos outros dois. Ele é baseado nos estudos de Bird & Hulstrom (1981 a, b), em que as equações de transmitâncias dos componentes atmosféricos foram desenvolvidas após uma comparação detalhada de vários modelos de insolação direta.
Para o modelo C descrito em Iqbal (1983), são utilizados como dados de entrada:
- latitude
- longitude
- dia do ano
- horário (com precisão de minutos)
- pressão atmosférica (para o cálculo da massa óptica de ar e comprimento óptico relativo ao ozônio)
- temperatura do ar (para o cálculo de pressão parcial do vapor d’água)
- umidade relativa do ar (para o cálculo de água precipitável)
- visibilidade horizontal (para o cálculo de transmitância do aerossol)
- grandezas adimensionais: albedo de superfície e de dispersão simples (fração da energia incidente espalhados atenuação total pelos aerossóis), fração de dispersão direta para dispersão total
De posse desses valores, são calculadas as transmitâncias devidas ao ozônio, à mistura de outros gases, ao vapor d’água e aos aerossóis, assim como o albedo de céu claro e os fatores astronômicos. Finalmente, a irradiância horizontal global sob céu sem nuvens é calculada como a soma de seus componentes diretos e difusos.
Linke turbidity factor – Dumortier
Em WMO (1981), o cálculo da turbidez atmosférica é realizado a partir de um valor média à superfície do mar com correções em quatro estágios sucessivos: correção por altura, umidade, aerossóis e elevação do sol. Os valores obtidos individualmente são somados ao valor médio para obtenção do TL final.
O fator de turbidez total (“Linke turbidity factor“, TL) resume a turbidez da atmosfera e, portanto, a atenuação da radiação solar direta do feixe. Ele é definido com base somente no tempo e espaço – ou seja, não precisa da definição de todas aquelas variáveis ambientais. É uma aproximação muito conveniente para modelar a absorção atmosférica e a dispersão da radiação solar de céu claro. Descreve a espessura óptica da atmosfera devido à absorção pelo vapor de água e à absorção e dispersão pelas partículas do aerossol em relação a uma atmosfera seca e limpa.
O TL denota a transparência da atmosfera sem nuvens. Quanto maior o TL, maior a atenuação da radiação pela atmosfera do céu claro. Ele é maior ao nível do mar do que em áreas montanhosas. Apresenta um comportamento sazonal, pois depende da quantidade de radiação solar e é influenciado por outros fatores de funcionamento periódico. Também aumenta com o nível de atividades industriais realizadas localmente. Se o céu estivesse perfeitamente seco e limpo, o TL seria igual a 1. Quando o céu estiver azul profundo, o TL estará logo acima de 1 e ainda será muito pequeno. No verão, na Europa, o vapor d’água é geralmente grande e o céu azul fica quase branco. O TL é maior que 3. Em atmosfera turva, como em cidades poluídas, o TL está próximo de 6 – 7.
O modelo que descreve as variações de turbidez foi desenvolvido por Dumortier (1998), mas também pode ser visto em Rigollier et al (2000). A componente direta é definida em Page (1996) e depende da massa óptica relativa do ar, dada por Kasten and Young (1989), e da profundidade óptica em uma atmosfera Rayleigh (contendo apenas moléculas de ar seco), dada por Kasten (1996). A componente difusa é definida em Dumortier (1995). Ambas as componentes dependem do fator de turbidez total (total turbidity factor), que descreve a atenuação da radiação solar devido ao vapor de água e aerossóis na atmosfera.
Seus valores climatológicos mensais foram calculados para todos os pontos do globo (resolução de aproximadamente 10 km) e estão disponíveis em imagens TIF no site do SODA (Solar Irradiation Data).
Comparação
A rede SONDA (Sistema de Organização Nacional de Dados Ambientais) do CCST (Centro de Ciências do Sistema Terrestre)/INPE (Instituto Nacional de Pesquisas Espaciais) disponibiliza séries temporais de dados meteorológicos (como irradiância, temperatura, pressão e umidade) de vários anos e diferente pontos do Brasil. Foram usados os dados para a estação de Brasília, Petrolina e São Martinho da Serra, entre os anos de 2012 e 2018. Os modelos foram calculados a cada 5 minutos.
Calculando-se o coeficiente de determinação entre os modelos, são encontrados valores entre 0,97 e 0,99 pra todos os anos e lugares. Assim, nota-se que os modelos são fortemente compatíveis. Como o comportamento é semelhante, seguem apenas os gráficos com valores para Brasília em 2012.
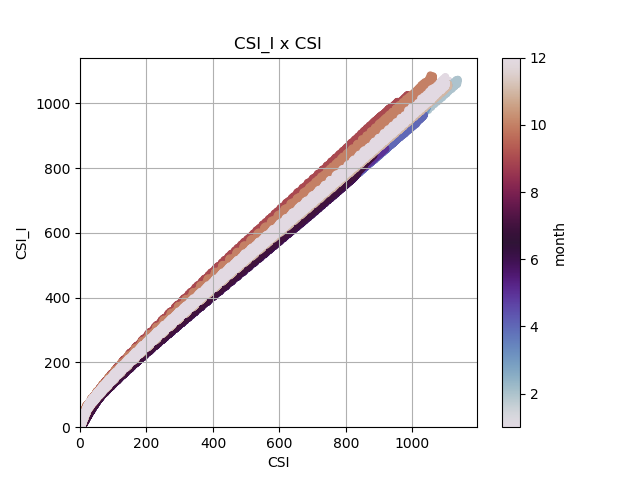
Em Brasília, as diferenças são maiores para os meses de agosto e setembro, quando os valores obtidos por Drumortier são sistematicamente menores que os calculados por Iqbal. Nesse sentido, não são observados comportamentos sistemáticos nos outros lugares.
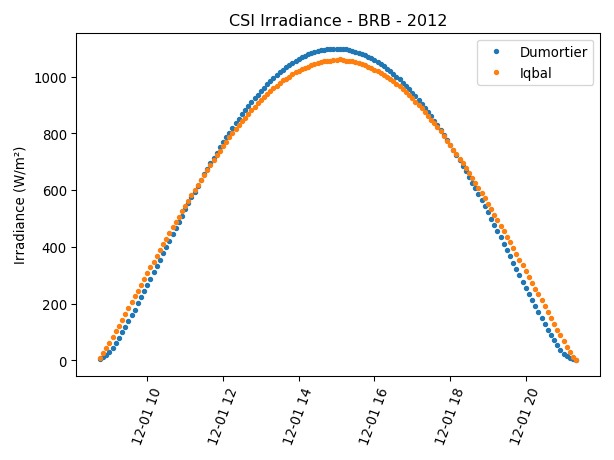
Os ciclos diurnos também apresentam comportamento semelhante entre todos os dias, anos e lugares. O exemplo a seguir refere-se ao dia 12 de janeiro de 2012 em Brasília. As maiores diferenças, que ainda são de poucas dezenas de W/m² no máximo, ocorrem em torno do meio-dia solar (Iqbal com valores menores), seguidas pelo pôr do sol e nascer do sol (Iqbal com valores maiores).
Ineichen & Perez
O trabalho de Ineichen & Perez (2002) propõem uma nova formulação para o coeficiente Linke turbidity com o objetivo de eliminar sua dependência da geometria solar. No processo, também desenvolvem dois novos modelos simples de céu claro para irradiância normal global e direta.
O coeficiente Linke turbidity tem a vantagem de ser amplamente utilizado desde 1922 (Linke, 1922) para quantificar esta informação, mas tem a desvantagem de ser dependente da massa de ar. O novo coeficiente inclui os efeitos dos aerossóis e do vapor de água. Esse modelo é implementado na biblioteca pvlib, sendo que um exemplo de uso está disponível no Github/ViniRoger – irradiance.
Fontes
- Bird R. and Hulstrom R. L. (1981 a), Direct insolation models, Transactions of the ASME Journal Solar Energy Engineering, 103, 182-192.
- Bird R. and Hulstrom R. L. (1981 b), A simplified clear sky model for direct and diffuse insolation on horizontal surfaces. Report SERI/TR-642-761, Solar Energy Research Institute, Golden, Colorado, U.S.A.
- Detailed Guide, Satel-Light. Disponível em: http://satellight.entpe.fr/guide/advirr.htm. Acesso em 23 de out. de 2019.
- Dumortier D. (1995), Mesure, analyse et modélisation du gisement lumineux. Application à l’évaluation des performances de l’éclairage naturel des bâtiments. Tese de doutorado, Université de Savoie, France, 350 pg.
- Dumortier D. (1998), The satellight model of turbidity variations in Europe. Ecole Nationale des Travaux Publics de l’Etat, Vaulx-en-Velin, France. Report for the sixth SATELLIGHT meeting in Freiburg, Germany, September 1998.
- Iqbal M. (1983), An introduction to Solar Radiation (New York: Academic Press), pp. 173-200.
- Kasten F. and Young A.T. (1989), Revised optical air mass tables and approximation formula. Applied Optics, 28, pp 4735-4738.
- Kasten F. (1996), The Linke turbidity factor based on improved values of the integral Rayleigh optical thickness. Solar Energy, 56, 3, pp 239-244.
- Linke F. (1922) Transmissions-Koeffizient und Trubungsfaktor. Beitr. Phys. fr. Atmos. 10, 91–103.
- Linke turbidity factor, SODA – Solar Irradiation Data. Disponível em: http://www.soda-pro.com/help/general-knowledge/linke-turbidity-factor. Acesso em 23 de out. de 2019.
- Page J. (1996), Algorithms for the Satellight programme, Technical Report for the second SATELLIGHT meeting in Bergen, Norway, June 1996.
- Pierre Ineichen, Richard Perez, A new airmass independent formulation for the Linke turbidity coefficient, Solar Energy, Volume 73, Issue 3, 2002, Pages 151-157, ISSN 0038-092X, https://doi.org/10.1016/S0038-092X(02)00045-2.
- WMO, 1981. Technical Note N° 172, WMO-No. 554, World Meteorological Organization, Geneva, Switzerland, pp. 121-123. Disponível em: https://library.wmo.int/index.php?lvl=notice_display&id=6311#.XbG3iHVKg5k. Acesso em 23 de out. de 2019.




One comment