As Sete Pontes de Königsberg são um problema historicamente notável em matemática. Sua resolução (negativa) por Leonhard Euler em 1736 lançou as bases da teoria dos grafos e prefigurou a ideia de topologia.
A cidade de Königsberg (atual Kaliningrado) é cortada pelo Rio Prególia, onde há duas grandes ilhas que, juntas, formam um complexo que na época continha sete pontes. Duas das sete pontes originais não sobreviveram ao bombardeio de Königsberg na Segunda Guerra Mundial. Mais tarde, outros dois foram demolidos e substituídos por uma estrada moderna. As outras três pontes permanecem, embora apenas duas sejam da época de Euler – uma delas foi reconstruída em 1935.
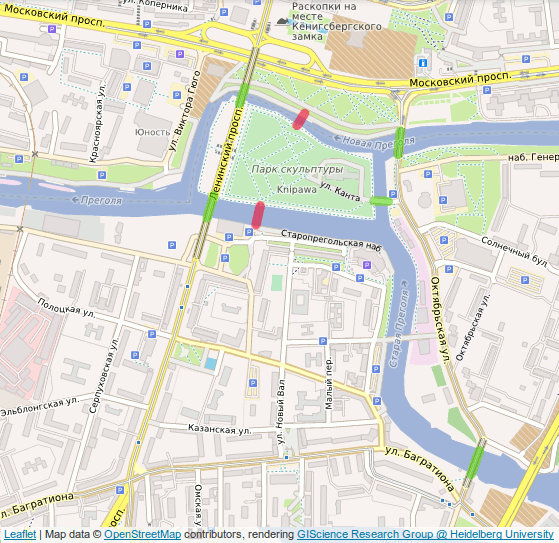
O problema era: como seria possível fazer um passeio a pé pela cidade de forma a passar uma única vez por cada uma das sete pontes e retornar ao ponto de partida?
Euler provou que esse problema não tem solução. A dificuldade que ele enfrentou promoveu o desenvolvimento de uma técnica adequada de análise e de testes subsequentes que estabeleceram essa afirmação com rigor matemático. Acompanhe essa análise e o surgimento de conceitos básicos na Teoria dos Grafos.
Análise de Euler
Euler eliminou os detalhes geométricos do problema, como o comprimento das pontes, a sua forma, o tamanho das ilhas, ou seja, descartou tudo que era irrelevante ao problema, colocando foco somente no que importava na rota. Com isso acabou representando o problema por uma abstração, que depois seria conhecida como grafo.
Um grafo é um desenho no qual temos alguns pontos e linhas ligando pares de pontos. No caso do problema das pontes, o grafo de Euler tem quatro pontos (ou vértices): uma das margens do rio, a outra margem, uma das ilhas e a outra ilha. Também possui sete linhas (ou arestas), que representam as pontes.

Euler observou também que, sempre que alguém entra em um vértice por uma ponte, deixa o vértice por outra ponte, exceto nos pontos finais da caminhada. Em outras palavras, durante qualquer caminhada no gráfico, o número de vezes que alguém entra em um vértice não terminal é igual ao número de vezes que ele sai dele.
Ao atravessar cada vértice, são gastos exatamente duas linhas: uma para entrar no ponto e outra para sair. Ou seja, cada vértice deve ter grau par de linhas. No entanto, todas as 4 massas de terra são tocadas por um número ímpar de pontes (uma é tocada por 5 pontes e cada uma das outras três é tocada por 3). Como, no máximo, duas massas terrestres podem servir como pontos finais de uma caminhada, a proposição de uma caminhada atravessando cada ponte leva a uma contradição.
Na linguagem moderna, Euler mostra que a possibilidade de percorrer um grafo, atravessando cada extremidade exatamente uma vez, depende dos graus dos nós. O grau de um nó é o número de arestas que o tocam. O argumento de Euler mostra que uma condição necessária para a caminhada da forma desejada é que o gráfico seja conectado e tenha exatamente zero ou dois nós de grau ímpar. Se houver nós de grau ímpar, qualquer caminho euleriano (caminho que usa apenas uma aresta de cada vez) começará em um deles e terminará no outro.
Teoria dos grafos
A teoria dos grafos é um ramo da matemática que estuda as relações entre os objetos de um determinado conjunto. Um grafo pode ser representado como G(E,V), onde:
- G é o grafo, um modelo de armazenamento de informações usado para representar uma dada relação entre alguns pares do universo de elementos armazenados;
- V é o conjunto de vértices (ou nós), unidades destinadas a guardarem todas as informações de um elemento desse universo;
- E é um subconjunto de pares não ordenados de V, que representa a existência da referida relação entre dois elementos desse universo.
Dependendo da aplicação, essas arestas podem ter orientação, chamado dígrafo e representado por uma seta, ou mesmo um peso (numérico) associado. Um fluxograma é um grafo orientado de sentido único. Existem grafos com definições e aplicações específicas.
Um ciclo é um passeio de comprimento mínimo três, em que o primeiro e o último vértice coincidem, mas nenhum outro vértice é repetido. Um grafo bipartido possui vértices que podem ser divididos em dois conjuntos disjuntos U e V tais que toda aresta conecta um vértice em U a um vértice em V, ou seja, U e V são conjuntos independentes. Um grafo planar é aquele que pode ser imerso no plano de tal forma que suas arestas não se cruzem.
Uma árvore é um grafo conexo (existe caminho entre quaisquer dois de seus vértices) e acíclico (não possui ciclos). Caso o grafo seja acíclico mas não conexo, ele é dito uma floresta, que também é definida como uma união disjunta de árvores. Toda árvore é um grafo bipartido e planar, podendo ser denominada enraizada se possuir um vértice escolhido como especial, denominado raiz. Clique é um subgrafo que também é um grafo completo.
Vértices incidentes à aresta ocorrem quando eles são conectados por uma aresta, sendo esses vértices considerados adjacentes entre si. As adjacências podem ser gravadas em uma matriz, que indica quais pares são adjacentes, ou em uma lista. O conjunto de vizinhos de um vértice consiste de todos os vértices adjacentes a ele. O grau de um vértice é o número de arestas incidentes a ele – se houver laços (aresta que conecta vértice a ele mesmo), serão contados duas vezes. Em um dígrafo, distingue-se o grau de saída (o número de arestas saindo de um vértice) e o grau de entrada (o número de arestas entrando em um vértice).
Um passeio entre dois vértices é uma lista alternada de vértices e arestas, sendo seu tamanho correspondente ao número de arestas que possui, incluindo as repetições. Já um caminho é uma sequência de vértices, de modo que cada vértice possui uma aresta para o vértice seguinte. Se nenhum dos vértices no caminho se repete, o caminho é dito simples, e se dois caminhos não têm vértices em comum, são ditos independentes.
Para percorrer todos os vértices e arestas do gráfico de um modo sistemático, esse percurso pode ser interpretado como colocar todos os nós em uma linha. Dentre os percursos básicos de busca em um grafo, estão a busca em largura (BFS), onde visita-se cada nó começando do menor nível e movendo-se para os níveis mais altos nível após nível, e a busca em profundidade (DFS), onde as visitas seguem por um certo caminho até atingir o alvo ou um nó que não possua filhos (nó folha).
Aplicações
Na coleta de lixo, entrega de mercadorias, conexão entre computadores, ligações entre artigos na internet e vários setores da economia devem realizar estudos usando grafos para descobrir a forma mais econômicas de interligar pontos, evitando caminhos desnecessários e gasto de energia. O desenvolvimento de algoritmos para manipular grafos é um tema importante da ciência da computação.
O problema do caminho mínimo consiste na minimização do custo de travessia de um grafo entre dois nós (ou vértices); custo este dado pela soma dos pesos de cada aresta percorrida, que podem ser armazenados em uma tabela. O problema do caixeiro viajante é um exemplo disso, no qual deve-se determinar a menor rota para percorrer uma série de cidades (visitando uma única vez cada uma delas), retornando à cidade de origem. Algoritmos específicos para várias aplicações foram desenvolvidos, como para encontrar caminhos mais rápidos em aplicativos de mapas. Se os vértices representam os estados de um quebra-cabeça como o Cubo de Rubik e cada borda direcionada corresponde a um único movimento ou turno, um algoritmo pode encontrar uma solução que use o número mínimo possível de movimentos.
O algoritmo de Ford-Fulkerson é empregado quando se deseja encontrar um fluxo de valor máximo, que faça o melhor uso possível das capacidades disponíveis na rede em questão. A história do algoritmo está relacionada à análise da rede ferroviária da União Soviética, mas já foi aplicada também em redes elétricas, transporte de fluidos e de dados em uma rede de computadores.
Um dos problemas mais conhecidos em teoria dos grafos é problema das quatro cores: dado um mapa plano, dividido em regiões, quatro cores são suficientes para colori-lo de forma a que regiões vizinhas não partilhem a mesma cor. Até hoje, ninguém conseguiu uma demonstração do teorema que não recorra a um computador.
Uma aplicação mais lúdica é através do jogo de tabuleiro “Snakes and Ladders”. Um grafo pode ser montado descrevendo o que acontece com o jogador ao cair em cada casa. O post do blog Grafosweb mostra como montar esse grafo e a matriz de adjacências, assim como calcular o grau dos vértices, as probabilidades de vitória de um jogador e quais casas do tabuleiro são mais prováveis de serem acessados.
Fontes
- Wikipedia – Seven Bridges of Königsberg, Teoria dos Grafos
- ITA – CES-11 Algoritmos e Estruturas de Dados (notas de aula de Grafos)