Existe um grande número de diferentes métodos de previsão baseados apenas na análise de valores passados de uma sequência de tempo. O principal instrumento desses métodos é o esquema de extrapolação, onde presume-se que as propriedades de sequência identificadas em um determinado de tempo passado serão as mesmas no passado e no futuro.
Os métodos de previsão com modelos de suavização baseiam-se na ideia de que observações passadas contêm informações sobre o padrão da série temporal, distinguindo o padrão de comportamento de eventuais ruídos. Um exemplo é o uso de Médias Móveis Simples (MMS) e ponderadas (que multiplica fatores para fornecer diferentes pesos para diferentes dados), muito utilizadas para estudar a volatilidade ao comparar médias de menor período (comprimento de média) com as de maior comprimento. No entanto, comportamentos muito antigos tem o mesmo peso de comportamentos mais recentes, correndo-se o risco de levar previsões próximas do comportamento médio de toda a amostra.
Suavização exponencial
Primeiramente, suponha um modelo simples no qual o processo simulado é a soma nível de processo variável e da média zero variável aleatória (tudo em função do tempo). É possível multiplicar o processo simulado por um valor entre 0 e 1, chamado de constante de suavização α . Com α = 0, não há suavização e o resultado será um valor constante para qualquer tempo; se α = 1, o nível do processo não sofre distorção, assim como o componente aleatório.
A Suavização Exponencial Simples (SES) pondera as observações passadas com pesos maiores às observações mais recentes, eliminando uma das desvantagens do método de MMS. Uma técnica similar a essa é a Suavização Exponencial de Holt (SEH), recomendada para séries que apresentam tendência – em vez de suavizar só o nível, gerando um erro sistemático, ele usa uma nova constante de suavização para “modelar” a tendência da série. Se a série também contiver sazonalidade, a recomendação vai para outra técnica. Veja também sobre tendência e sazonalidade clicando no link.
A Suavização Exponencial de Holt-Winters (HW) envolve três equações com três parâmetros de suavização que são associados a cada componente da série: nível, tendência e sazonalidade. Existem variações dessa técnica: tanto o termo de sazonalidade quanto o de tendência pode ser adicionado e/ou multilplicado ao nível de processo variável, de modo normal ou amortecido. As 15 variações decorrentes desses cenários podem ser vistas em tabela do link, com as fórmulas para cálculos recursivos e previsões pontuais – em cada caso, lt denota o nível da série no tempo t, bt denota a inclinação no tempo t, st é a componente sazonal da série no tempo t e m é o número de estações em um ano, enquanto que α, β, γ e φ são os parâmetros de suavização.
Ainda nesse texto do link, a terminologia utiliza letras para identificar o tipo de erro, de tendência e de sazonalidade, respectivamente. Essas letra são as seguintes:
- N = nenhum (exceto para erro)
- A = aditivo
- M = multiplicativo
- d = amortecimento (em conjunto com A ou M)
- Z = escolha automática
Por exemplo, “ANN” é suavização exponencial simples com erros aditivos e “MAM” é o método multiplicativo de Holt-Winters com erros multiplicativos. Para escolher se é amortecido ou não, usar o argumento “dumped”: se TRUE, usa uma tendência amortecida (aditivo ou multiplicativo); se NULL, tendências tanto amortecidas como não amortecidas serão testadas e retornará o melhor modelo (de acordo com o critério de informação ic) retornado.
No R, a função ets() do pacote forecast calcula a suavização exponencial recebendo como argumento um vetor numérico ou uma série temporal (convertida pela função ts()). Além disso, deve-se informar o critério de informação “ic” utilizado para realizar a escolha de modelos (“aicc”,”aic”,”bic”) e três letras identificando o método a ser utilizado (“model”) conforme os códigos apresentados anteriormente. Também permite entrar como argumento os valores de α, β, γ e φ assim como outros parâmetros. Exemplo de uso: model = ets(dados.ts, model=”ZZZ”, damped = TRUE, ic=’aic’)

| (E,T,S) | AIC | ME | RMSE | MAE | MPE | MAPE | MASE | ACF1 |
|---|---|---|---|---|---|---|---|---|
| (M,Md,M) | 305.733 | -5.656 | 60.138 | 49.683 | -0.856 | 4.639 | 0.464 | -0.162 |
Visualmente, os dados observados apresentam sazonalidade anual, apesar de não ter muitos valores para confirmar com mais certeza. Assim, todas as combinações envolvendo o último termo como “N” resultaram em linhas retas horizontais ou com tendência de subida. Deixando tudo no automático, a escolha é ETS(M,Md,M).
Veja mais informações sobre a interpretação e como são calculadas as medidas de acurácia (MAE, MSE, MAPE, MASE) no post Métricas para comprar previsões.
ETS vs ARIMA
O modelo autorregressivo integrado de médias móveis (ARIMA) é uma generalização de um modelo de média móvel autorregressiva (ARMA). A diferença entre estes dois modelos é o uso de um termo de integração que precisa diferenciar as séries temporais (subtraindo a observação no período corrente do anterior), deixando-as estacionárias – condição necessária para operar com um modelo assim. Os parâmetros de um modelo ARIMA são três (p, d, q) e representam respectivamente o parâmetro autorregressivo, o parâmetro de integração e a média móvel. A melhor maneira de escolher os parâmetros é usar a técnica Box-Jenkins (1971), analisando a função de autocorrelação (ACF) e a função de autocorrelação parcial (PACF) das séries temporais diferenciadas.
Apesar de propostos por Holt e Brown bem antes dos trabalhos de Box e Jenkins, os modelos lineares de suavização exponencial são todos casos especiais de modelos ARIMA. Já os modelos de suavização exponencial não linear não têm equivalentes equivalentes ARIMA. Há também muitos modelos ARIMA que não têm equivalente de suavização exponencial. Em particular, todo modelo ETS não é estacionário, enquanto que os modelos ARIMA podem ser estacionários. A tabela do link apresenta algumas relações de equivalência para as duas classes de modelos.

Resultado dos testes de estacionariedade e de tendência:
- ADF: 0.2285
- KPSS: 0.0798
- Runs: statistic = -2.0871, runs = 8, n1 = 12, n2 = 12, n = 24, p-value = 0.03688
- Cox Stuart: statistic = 9, n = 12, p-value = 0.146
- Mann-Kendall Rank: statistic = 1.8851, n = 24, p-value = 0.05941
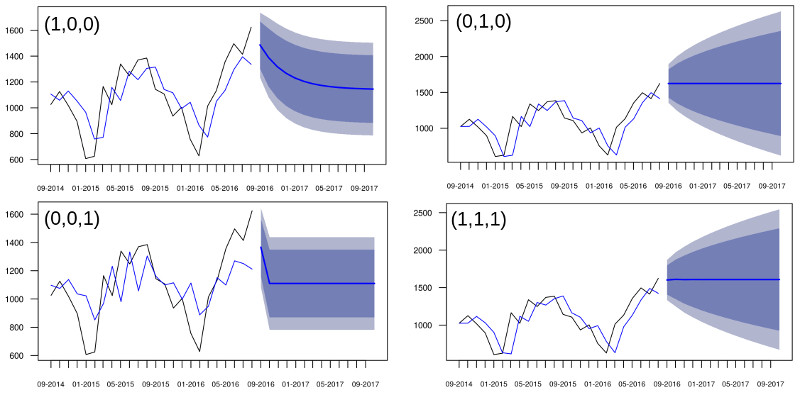
Estatísticas dos modelos e projeções:
| (p,d,q) | AIC | ME | RMSE | MAE | MPE | MAPE | MASE | ACF1 |
|---|---|---|---|---|---|---|---|---|
| (1,0,0) | 328.050 | 4.848 | 195.468 | 164.991 | -3.636 | 16.852 | 1.539 | 0.066 |
| (0,1,0) | 313.130 | 24.959 | 205.083 | 163.126 | -0.365 | 15.849 | 1.522 | -0.087 |
| (0,0,1) | 332.900 | 1.735 | 217.292 | 176.351 | -5.053 | 18.015 | 1.645 | 0.172 |
| (1,1,1) | 316.900 | 26.014 | 204.029 | 161.094 | -0.436 | 15.722 | 1.503 | 0.010 |
A função auto.arima() retorna o modelo com menor AIC – nesse caso, o modelo escolhido foi o ARIMA(1,0,0). No entanto, tá na cara que essas projeções estão furadas! Isso porque a série tem uma parte sazonal, conforme mencionado ao falar de ETS, que deve ser incluída no modelo.
A parte sazonal de um modelo ARIMA tem a mesma estrutura que a parte não sazonal: ARIMA(p,d,q)x(P,D,Q) onde P é o número de termos sazonais autorregressivos, D é o número de diferenças sazonais, Q é o número de termos de média móvel sazonal.
Assim, aplicou-se diferenciação “D=1” na parte sazonal como outro argumento na função auto.arima(), obtendo-se o modelo “ARIMA(0,0,0)(0,1,0)[12] with drift”:

Estatísticas dos modelos e projeções
| (p,d,q)x(P,D,Q) | AIC | ME | RMSE | MAE | MPE | MAPE | MASE | ACF1 |
|---|---|---|---|---|---|---|---|---|
| (0,0,0) | 340.83 | -3.031533e-13 | 269.9837 | 215.3611 | -7.407961 | 22.68479 | 2.00959 | 0.6318802 |
| (0,0,0)(0,1,0) | 151.97 | 0.5168921 | 81.45377 | 48.76689 | -0.4894911 | 4.476549 | 0.4550565 | -0.08943678 |
Caso o termo “D” não seja informado, será aplicado o resultado do teste OCSB. Havendo necessidade de diferenciação na parte não-sazonal (decidida através do teste KPSS), haveria mudança no valor de “d”, mas também poderia ser colocado usando como argumento “d=1” na função para diferenciação de ordem 1. Exemplo de uso: auto.arima(dados.ts, D=1)
O pacote forecast não tem como incluir regressores usando ETS – uma outra formulação para incluir regressores foi proposta em um trabalho comentado no link, mas é mais confusa e difícil de interpretar do que usar um modelo ARIMA. Ele também não ajusta um modelo ARIMA com sazonalidade maior do que 350 (fonte) – pode-se usar termos de Fourier para a sazonalidade e erros ARMA para a dinâmica de curto prazo.
De modo geral, quanto mais curto o intervalo de observação disponível, maior é a probabilidade de se ter uma visão errada em relação ao processo como um todo. Por outro lado, ao fazer uma previsão de curto prazo, a redução do tamanho da amostra pode conduzir ao aumento da precisão de tal previsão. Por exemplo: fazer uma previsão de tempo usando diretamente uma grande série climatológica pode levar às previsões serem próximas à média climatológica, dando um peso muito baixo às variações mais recentes, podendo inclusive suavizar demasiadamente extremos meteorológicos.
Outro aspecto para se considera em previsões: quanto maior o intervalo de previsão, mais forte o efeito da variabilidade das características de sequência sobre o erro de previsão.
Fontes
- A comparison of forecast models to predict weather parameters
- Portal Action – Modelos de suavização exponencial
- MQL5 – Previsão de séries temporais utilizando suavização exponencial
- Renato Vieira dos Santos – Uma Aplicação de Métodos de Renormalização ao Estudo de Séries Temporais Financeiras
- Rob Hyndman & George Athanasopoulos – Holt-Winters seasonal method
- Rob Hyndman & George Athanasopoulos – Evaluating forecast accuracy
- Robert Nau – What’s the bottom line? How to compare models
- Robert Nau – What’s a good value for R-squared?


2 comments