Considere a seguinte situação: você criou um modelo matemático para analisar imagens e detectar interferências, de modo a automatizar uma tarefa que manualmente seria muito demorada e trabalhosa. Para validar o modelo, é necessário verificar visualmente pelo menos uma amostra dessas imagens para saber se estão ou não com interferências. Analisar muitas imagens demanda muito tempo; para poucas imagens mais é fácil, porém é muito provável pegar um subconjunto sem a mesma significância para todo o resto. Então, qual o número de amostras deve-se considerar?
A significância estatística é um conceito que ajuda a determinar se os resultados de uma análise ou experimento são significativos ou se ocorreram por acaso. Quando um resultado é estatisticamente significativo, significa que há evidências suficientes para rejeitar a hipótese nula (geralmente, a hipótese de que não há efeito ou diferença) e acreditar que o efeito observado é real e não apenas fruto de variações aleatórias nos dados.
A significância estatística é frequentemente medida por um valor-p (p-value), que representa a probabilidade de se obter o resultado observado (ou algo mais extremo) se a hipótese nula for verdadeira. Se o valor-p for menor que um nível de significância previamente definido (geralmente 0,05, ou 5%), o resultado é considerado estatisticamente significativo. Isso significa que a chance de o efeito observado ter ocorrido apenas por acaso é menor que 5%. Veja mais sobre Testes de Hipóteses e de Aderência, assim como p-valor, no post do link.
Um papel essencial da significância estatística está em garantir a validade dos resultados de pesquisas, estudos experimentais, ou análises de dados. Seu principal objetivo é ajudar a evitar falsos positivos, ou seja, conclusões que indicam a existência de um efeito quando ele não existe.
Na medicina, por exemplo, novos tratamentos são aprovados apenas se os ensaios clínicos mostrarem resultados estatisticamente significativos de que o tratamento é eficaz, em vez de melhorias que poderiam ter ocorrido por sorte. Em muitos setores, as decisões sobre onde alocar recursos (tempo, dinheiro, equipe) dependem de análises estatisticamente significativas. Por exemplo, em uma pesquisa de mercado, uma empresa pode decidir investir em uma nova estratégia se houver evidências estatísticas de que essa abordagem aumentará as vendas.
É importante lembrar que a significância estatística não garante a relevância prática. Um resultado pode ser estatisticamente significativo, mas o efeito pode ser pequeno demais para ser relevante na prática. Além disso, um valor-p pequeno não prova que a hipótese nula é falsa, apenas indica que é improvável que os resultados observados sejam devidos ao acaso. Da mesma forma, a ausência de significância estatística não prova que um efeito não existe — pode ser que o tamanho da amostra seja muito pequeno para detectar o efeito.
Tamanho da amostra
Para determinar o número de amostras, existe uma fórmula baseada na distribuição normal e na variância da proporção amostral para estimar um parâmetro da população. Especificamente, ela vem da fórmula da variância para uma proporção:
\(
Var(\hat{p}) = \frac{{p(1 – p)}}{n}
\)
Ao rearranjar essa fórmula para resolver para n (tamanho da amostra) em termos de parâmetros que podem ser definidos para cada caso, obtém-se a seguinte equação:
\(
n = \frac{{Z^2 \cdot p \cdot (1-p)}}{{E^2}}
\)
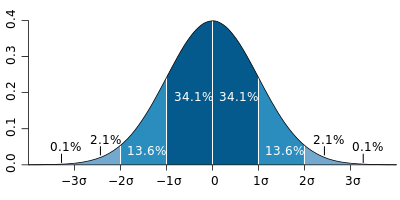
– O valor Z é o número de desvios padrão que corresponde ao nível de confiança desejado, obtido da distribuição normal. Para um nível de confiança de 95%, o valor Z é 1,96. Ele vem da curva normal padrão, onde aproximadamente 95% dos dados estão dentro de 1,96 desvios padrão da média. Um nível de confiança de 95% significa que, se você repetisse o estudo várias vezes, em 95% das vezes as conclusões obtidas estariam corretas, e apenas em 5% das vezes (nível de significância de 0,05 ou 5%) você obteria um resultado que poderia ser explicado pelo acaso.
– p é a proporção esperada da característica de interesse na população (neste caso, imagens com interferências). Quando não se conhece essa proporção, usa-se o valor conservador de 0,5 (50%), pois maximiza o tamanho da amostra. Como interferências são eventos relativamente raros, pode-se considerar que 10% das imagens têm interferências, ou seja, p = 0.10.
– E é a margem de erro, ou seja, o quanto você está disposto a deixar a estimativa variar da realidade da população. Para uma margem de erro de 3%, o valor E é 0,03. Essa margem representa o quão precisa a sua estimativa precisa ser em relação ao verdadeiro valor da população. Quanto menor a margem de erro (neste caso, 3%), maior será a amostra necessária para garantir que a estimativa da amostra esteja próxima do valor real da população.
– O termo p(1-p) é a variância binomial, ou seja, a variabilidade esperada na proporção de imagens com interferência e sem interferência. Ele reflete a incerteza sobre a presença ou não da característica de interesse. Uma maior variabilidade na população pode exigir um tamanho de amostra maior para garantir que os resultados observados sejam realmente significativos.
– Por fim, o termo E² é usado para ajustar a margem de erro em relação à variação total. Ele aparece no denominador porque, quanto menor a margem de erro desejada, maior precisa ser a amostra.
Exemplo: Aplicando todos esses valores, para um conjunto de 850646 imagens, ao menos 385 delas devem ser verificadas visualmente para validar o algoritmo com significância estatística.
Assim, a fórmula do tamanho da amostra deve garantir que, ao fazer inferências sobre a população, os resultados tenham significância estatística. Ou seja, o tamanho da amostra calculado com base na fórmula ajuda a garantir que você tenha dados suficientes para que os resultados não sejam atribuíveis ao acaso, mas sim refletem um efeito real (caso exista). Isso com uma determinada precisão (margem de erro) e confiabilidade (nível de confiança).
