Em matemática, a interpolação é um método que permite construir um novo conjunto de dados a partir de um conjunto discreto de dados pontuais previamente conhecidos. É muito usado para descobrir os valores entre números já conhecidos, o que permite desenhar mapas mais detalhados ou aumentar o número de dados em uma amostra. Para obter essa continuidade, pode-se construir uma função que aproximadamente se “encaixe” nestes dados pontuais.
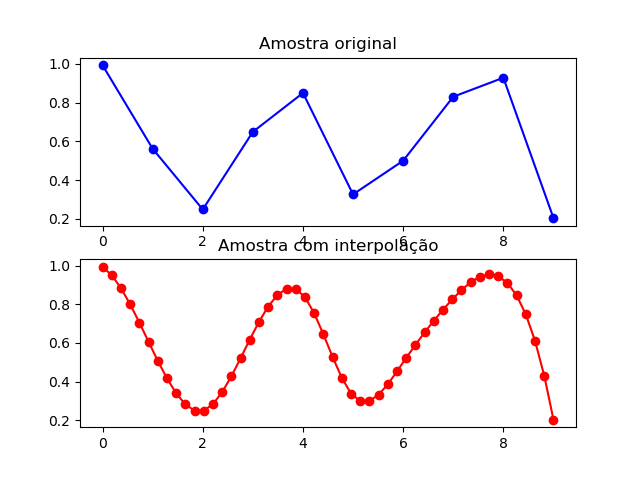
No python, os pacotes numpy e SciPy possuem métodos de interpolação (interp e interpolate, respectivamente). Veja esse exemplo prático para aumentar uma série de 10 para 50 amostras (fonte: stackoverflow):
#!/usr/bin/env python3.7.6
# -*- Coding: UTF-8 -*-
import numpy as np
import scipy.interpolate as interpolate
import matplotlib.pyplot as plt
# Fix seed - optional
#import random
#random.seed(123)
# Generate some random data
y = np.random.random(10)
x = np.arange(y.size)
# Interpolate the data using a cubic spline to "new_length" samples
new_length = 50
new_x = np.linspace(x.min(), x.max(), new_length)
new_y = interpolate.interp1d(x, y, kind='cubic')(new_x)
# Plot the results
plt.figure()
plt.subplot(2,1,1)
plt.plot(x, y, 'bo-')
plt.title('Amostra original')
plt.subplot(2,1,2)
plt.plot(new_x, new_y, 'ro-')
plt.title('Amostra com interpolação')
plt.show()
A primeira parte visa fixar uma semente (opcional) e então gerar um vetor com valores 10 valores randômicos (eixo y) e uma sequência numérica com o mesmo tamanho do primeiro vetor (eixo y). Na segunda parte, são criados dois vetores: um novo eixo x, com o tamanho definido na variável “new_length”, e um novo eixo y interpolado usando os vetores dos eixos x e y originais, com base no novo eixo x. Por fim, são plotadas as duas curvas.
Foi usada a interpolação cúbica, que é muito versátil para vários tipos de problemas, mas existem outros tipos: ‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’, ‘previous’, ‘next’, where ‘zero’, ‘slinear’, ‘quadratic’ e ‘cubic’.