Existem diversos métodos matemáticos e ferramentas no python para ajustar uma função pré-definida a um conjunto de dados, de modo a calcular seus coeficientes. Esse post tem como objetivo ilustrar alguns dos principais métodos com exemplos práticos.
O numpy possui um método de ajuste polinomial para um certo grau informado, conforme o exemplo a seguir:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([ 3.08, 3.1 , 3.12, 3.14, 3.16, 3.18, 3.2 , 3.22, 3.24,
3.26, 3.28, 3.3 , 3.32, 3.34, 3.36, 3.38, 3.4 , 3.42,
3.44, 3.46, 3.48, 3.5 , 3.52, 3.54, 3.56, 3.58, 3.6 ,
3.62, 3.64, 3.66, 3.68])
y = np.array([ 0.000857, 0.001182, 0.001619, 0.002113, 0.002702, 0.003351,
0.004062, 0.004754, 0.00546 , 0.006183, 0.006816, 0.007362,
0.007844, 0.008207, 0.008474, 0.008541, 0.008539, 0.008445,
0.008251, 0.007974, 0.007608, 0.007193, 0.006752, 0.006269,
0.005799, 0.005302, 0.004822, 0.004339, 0.00391 , 0.003481,
0.003095])
deg = 2
z = np.polyfit(x, y, deg)
y2 = np.poly1d(z)
plt.plot(x, y, "*")
plt.plot(x, y2(x), "-")
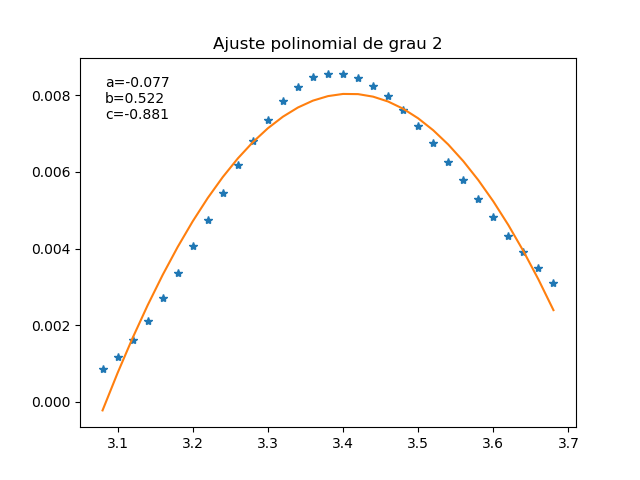
plt.title('Ajuste polinomial de grau 2')
plt.show()
A classe polyfit usa o método dos mínimos quadrados para ajustar um polinômio de grau “deg” (2, no caso) em um conjunto de dados “x vs y”. Já a classe poly1d permite calcular o novo vetor y (valores ajustados para cada valor de x).
O SciPy possui a classe “optimize”, cujo método curve_fit calcula os coeficientes para uma função objetivo, definida pelo programador. Veja o exemplo a seguir, usando os mesmos dados:
#!/usr/bin/env python3.7.6
# -*- Coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.optimize import minimize
def func(x, a, b, c):
return a*x**2 + b*x + c
x = np.array([ 3.08, 3.1 , 3.12, 3.14, 3.16, 3.18, 3.2 , 3.22, 3.24,
3.26, 3.28, 3.3 , 3.32, 3.34, 3.36, 3.38, 3.4 , 3.42,
3.44, 3.46, 3.48, 3.5 , 3.52, 3.54, 3.56, 3.58, 3.6 ,
3.62, 3.64, 3.66, 3.68])
y = np.array([ 0.000857, 0.001182, 0.001619, 0.002113, 0.002702, 0.003351,
0.004062, 0.004754, 0.00546 , 0.006183, 0.006816, 0.007362,
0.007844, 0.008207, 0.008474, 0.008541, 0.008539, 0.008445,
0.008251, 0.007974, 0.007608, 0.007193, 0.006752, 0.006269,
0.005799, 0.005302, 0.004822, 0.004339, 0.00391 , 0.003481,
0.003095])
popt, pcov = curve_fit(func, x, y)
fig, ax = plt.subplots()
plt.plot(x, y, '*')
plt.plot(x, func(x, *popt))
textstr = 'a=%5.3f\nb=%5.3f\nc=%5.3f' %tuple(popt)
ax.text(0.05, 0.95, textstr, transform=ax.transAxes, fontsize=10,
verticalalignment='top')
plt.title('Ajuste polinomial de grau 2')
plt.show()
A função “func” foi definida como uma função de grau 2, gerando os mesmos resultados que o exemplo com o numpy.
O método minimize (“out = minimize(j, coef, method=’BFGS’)”, por exemplo) recebe um vetor com um chute inicial de valores para cada um dos coeficientes (“coef = [1, 1., 0]”) e uma função objetivo “j” que define como deve ser a minimização (“return abs((y – func(x, *coef)).sum())”).


Olá, como fazer ajuste polinomial manualmente? Pode fazer um exemplo?
Olá Oliver, para fazer um ajuste polinomial manualmente, dado um conjunto de pontos (vetor x), eu calcularia o vetor y usando uma função de grau n e que tivesse uma aparência visual aos dados. Nesse exemplo, calcularia uma função de grau 2, já que parece com uma parábola, e faria um chute inicial dos coeficientes a e b. Para mensurar o avanço, calcularia o somatório da diferença quadrática entre os pontos calculados e observados, para cada par escolhido de coeficientes. Essa mudança na escolha de coeficientes pode ser automatizada, pegando de um vetor para a e outro para b, e imprimir o erro de cada caso, para então escolher o par de coeficientes que tenha o menor erro – processo esse que também pode ser automatizado.