Distribuição gama

A distribuição normal é uma das distribuições de probabilidade mais utilizadas para modelar fenômenos naturais, mas existem outras. A distribuição gama é uma família de distribuições contínuas de probabilidade de dois parâmetros. É usada para modelar valores de dados positivos que são assimétricos à direita e maiores que zero. É muito utilizada em Meteorologia, para descrever distribuição de precipitação, e em engenharia, para obtenção do tempo de retorno de um equipamento com falha.

Enquanto que uma distribuição normal é caracterizada por sua média e desvio padrão, uma distribuição gama usa outros parâmetros. A parametrização usando alpha e beta é mais comum em estatística bayesiana, enquanto que usando k e \(\theta\) é mais comum em econometria. Considera-se \(k=\alpha\) e \(\beta=1/\theta\), este conhecido como parâmetro de escala inversa ou taxa (“rate”). Sua função densidade de probabilidade pode ser escrita como:

\(f(x;\alpha,\beta)=\frac{\beta^\alpha x^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)}\)

com a função gama no denominador descrita como:

\(\Gamma(\alpha)=(\alpha-1)!\)

A função gama é uma extensão analítica da função fatorial para o conjunto dos números reais e complexos, sendo uma solução para o seguinte problema de interpolação: encontrar uma curva suave que conecte os pontos (x, y) dados por y = (x − 1)! em que x é um inteiro positivo.

O parâmetro de forma (k) indica o formato geral da curva. Quanto maior o valor de k, mais a distribuição tende a se aproximar de uma gaussiana. No gráfico a seguir, isso pode ser notado pelas curvas preta, vermelha, verde e azul (respectivamente), que apresentam somente o parâmetro de forma variando de modo crescente. Se k é um inteiro positivo, então a distribuição representa uma distribuição Erlang; para k = 1, a distribuição gama será simplificada para a distribuição exponencial.

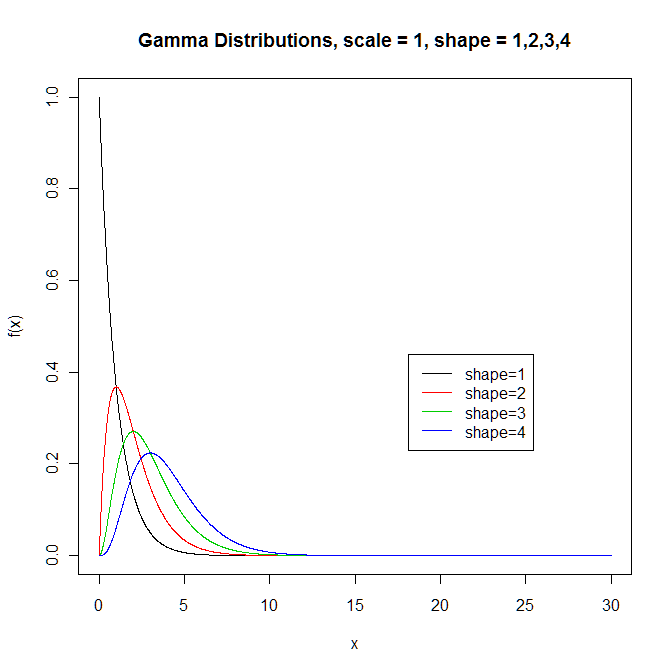
Função densidade de probabilidade de distribuições gama variando o parâmetro de forma (com o parâmetro de escala fixo). Fonte: clayford.net

O parâmetros de escala (\(\theta\)) indica o escalonamento da curva, ou seja, o quanto ela pode “esticar” ou “encolher” para cima (eixo y), dependendo das magnitudes gerais dos valores dos dados representados. Note que as curvas preta, vermelha, verde e azul (respectivamente) ficam mais “baixas” quanto maior o parâmetro de escala.

Função densidade de probabilidade de distribuições gama variando o parâmetro de escala (com o parâmetro de forma fixo). Fonte: clayford.net

Muitas distribuições comumente usadas para modelos paramétricos na análise de sobrevivência (como a distribuição Exponencial, a distribuição Weibull e a gama Gamma) são casos especiais da gama generalizada. A distribuição de Pearson do tipo III é uma distribuição gama generalizada de três parâmetros, que por sua vez é uma generalização da distribuição gama de dois parâmetros.

A distribuição log-normal é um caso especial da distribuição log-Pearson tipo III quando o coeficiente de assimetria/ distorção “skew” (Cs) dos dados logarítmicos é igual a 0. Quando o skew é positivo significa que a distorção é para a esquerda e quando negativo a distorção é para a direita. Essa distribuição e a de Gumbel são muito usadas para inundações máximas anuais.

Interpretação – processo de Poisson

O processo de Poisson é um tipo de objeto matemático que lida com a aleatoriedade e que consiste numa série de pontos dispostos no espaço matemático, com propriedades convenientes. Ele é utilizado para modelar eventos aleatórios, como a chegada de clientes em uma loja, distribuída no tempo. Esse estudo faz parte da teoria das filas, cujo objetivo é o de prover modelos para demonstrar previamente o comportamento de um sistema que oferece serviços cuja demanda cresce aleatoriamente, tornando possível dimensioná-lo de forma a satisfazer os clientes e também ser viável economicamente para o provedor do serviço, evitando desperdícios e gargalos.

A distribuição de Poisson é uma distribuição de probabilidade de uma variável aleatória discreta que expressa a probabilidade de uma série de eventos ocorrer num certo período de tempo, desde que estes eventos ocorram independentemente de quando ocorreu o último evento. A distribuição de Poisson aparece em vários problemas físicos, com a seguinte formulação: considerando uma data inicial (t = 0), seja N(t) o número de eventos que ocorrem até uma certa data t. Veja alguns exemplos:

N(t) pode ser um modelo para o número de impactos de asteroides maiores que um certo tamanho desde uma certa data de referência
Considere que o número de ligações para a polícia em uma cidade específica chegue a uma taxa de 3 por hora. O intervalo das 19:00 às 20:00 é independente das 20:00 às 21:00. O número esperado de chamadas para cada hora é 3. A distribuição Poisson nos permite encontrar, a probabilidade de o número da polícia da cidade receber mais de 5 ligações na próxima hora ou a probabilidade de eles não receberem chamadas nas próximas 2 horas.
Ainda nesse exemplo, para saber quanto tempo até a próxima ligação chegar, isso envolve investigar o tempo até a primeira alteração em um processo de Poisson. Se os eventos de um processo ocorrerem a uma taxa de 3 por hora, provavelmente esperamos esperar cerca de 20 minutos para o primeiro evento (3 por hora implica uma vez a cada 20 minutos). Mas qual é a probabilidade do primeiro evento em até 20 minutos? Ou dentro dos próximos 5 minutos? Ou mesmo depois de 30 minutos?
Suponha que exista 63% de probabilidade de assistir ao primeiro evento em 5 minutos, mas apenas 16% de chance de assistir a um evento nos próximos 5 minutos. A probabilidade exponencial (primeira), que é a distribuição dos tempos até a primeira mudança no processo de Poisson, indica a chance de esperarmos menos de 5 minutos para ver o primeiro evento, o que inclui todos os momentos antes de 5 minutos (2 minutos, 30 segundos, etc). Já a probabilidade de Poisson (segunda) indica a chance de observarmos exatamente um (1) evento nos próximos 5 minutos. Portanto, existe uma boa chance de se observar o primeiro evento em até 5 minutos, mas pouca chance de que seja apenas 1 evento.

Uma interpretação da distribuição gama é que seja a distribuição teórica dos tempos de espera ATÉ a k-ésima mudança para um processo de Poisson. Nos gráficos apresentados no item anterior, k (forma) é o número de eventos e \(\theta\) (escala) é o tempo médio de espera entre eventos. A primeira figura matem o tempo de espera em 1 e altera o número de eventos. A probabilidade de esperar 5 minutos ou mais aumenta à medida que o número de eventos aumenta. Isso é intuitivo, pois parece mais provável esperar 5 minutos para observar 4 eventos do que esperar 5 minutos para observar um evento, assumindo um tempo de espera de 1 minuto entre cada evento.

A segunda figura mantém o número de eventos em 4 e altera o tempo de espera entre os eventos. A probabilidade de esperar 10 minutos ou mais aumenta à medida que o tempo entre os eventos aumenta. Isso é bastante intuitivo, pois você esperaria uma maior probabilidade de esperar mais de 10 minutos para observar 4 eventos quando houver um tempo médio de espera de 4 minutos entre os eventos versus um tempo médio de espera de 1 minuto.

O cálculo do período de retorno de enchentes segue um pouco dessa lógica, mas usando a distribuição de Gumbel – veja mais no post Estatística em Hidrologia.

Para calcular a probabilidade, é necessário fazer uma transformação para re-escalonar a variável X de interesse para a variável, dividindo-se seu valor (X) pelo parâmetro de escala. O passo seguinte é consultar a tabela com pontos percentuais da distribuição gama com parâmetro de escala unitária (disponível no link). Busca-se a coluna com o valor do parâmetro de forma e a linha dessa coluna que contém a razão previamente calculada (X/\(\beta\)). Seguindo-se essa linha até a coluna com a probabilidade acumulada, esse será o valor da probabilidade de ocorrer o valor X. O complementar desse valor (1-X) é a probabilidade de que ocorra um valor acima dele. Por exemplo, considerando-se que uma precipitação de x = 80 mm tenha uma probabilidade acumulada de 0.88, isso significa que existe 88% de chance de chover até 80 mm e 12% de chover mais do que esse valor.

Implementação em python

Uma das formas de descobrir se um conjunto de dados possui distribuição gama é fazendo um histograma para verificar a distribuição de valores. Isso pode ser feito através do pacote matplotlib, usando o método “hist” – basta informar os dados e a distribuição dos bins. No pacote SciPy, o método “gamma.fit” permite estimar os valores dos parâmetros de forma e de escala, mas você pode calculá-los através dos estimadores de Thom-Thom, conforme o código a seguir:

@staticmethod
def gamma_parameters(data):
	"""
	Calculate gamma PDF parameters shape (a) and scale (b)
	:parameter list data: input data
	"""
	import math
	n = len(data)
	ave = sum(data)/n
	sum_ln = sum(math.log(x) for x in data)
	d = math.log(ave) - (1/n)*sum_ln
	a = (1 + math.sqrt(1 + (4*d)/3))/(4*d)
	b = ave/a
	return a, b

Todas as distribuições contínuas no scipy.stats possuem parâmetros de localização (“location”) e escala (“scale”), mesmo aqueles para os quais o local geralmente não é usado. Para a distribuição gama, basta deixar o “location” com o valor padrão 0. Se você estiver usando o método de ajuste (“fit”), use o argumento floc = 0 para garantir que ele não trate o local como um parâmetro livre.

Função de distribuição acumulada

A função distribuição acumulada (ou CDF, do inglês cumulative distribution function) de uma variável real X é a probabilidade desse X assumir um valor menor ou igual a \(x_0\), também conhecido como limiar ou threshold. Em um gráfico da probabilidade em função de X, as probabilidades (eixo y) são somadas a cada avanço nos valores de X (eixo x). Difere da função densidade de probabilidade (FDP), que é uma função que descreve a probabilidade relativa de uma variável aleatória tomar um valor dado.

Para se obter a probabilidade acumulada para que um valor seja menor ou igual a x, existe o método “gamma.cdf”; para a probabilidade que o valor seja maior que x, é o método “gamma.sf” (survival function). Elas admitem os parâmetros floc e fscale para forçar uma estimativa de parâmetro do ajuste.

Exemplo de gráfico com pontos calculados usando uma função de distribuição acumulada ajustada para uma amostra com distribuição gama

O método a seguir recebe uma lista de valores como entrada para ajustar uma função gama e, com os parâmetros de forma e de escala calculados, calcular a função de distribuição acumulada para fazer um gráfico dela. Como saída, será impresso na tela um gráfico das probabilidades acumuladas em função dos valores da lista.

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

def cdf_gamma(lst):
	cdf_x = np.linspace(start=0, stop=max(data), num=len(data))
	# Y axis
	param = stats.gamma.fit(lst)
	shape = param[0]
	scale = param[2]
	cdf_y = stats.gamma.cdf(cdf_x, *param)

	# Plot CDF
	plt.plot(lst, cdf_y, '*')
	plt.show()

O método “linspace” do numpy cria uma sequência de números uniformemente espaçados entre os limites “start’ e “stop”, com um número “num” de pontos.

Fontes