O nome k-NN vem de “k-Nearest Neighbor” (k-ésimo vizinho mais próximo), ou seja, esse método de machine learning tem como objetivo classificar x_t atribuindo a ele o rótulo representado mais frequentemente dentre as k amostras mais próximas e utilizando um esquema de votação. O que determina essa “proximidade entre vizinhos” é uma distância calculada entre pontos em um espaço euclidiano (instâncias), cujas fórmulas mais comuns são a distância Euclidiana e a distância Manhattan.
O “Center for Machine Learning and Intelligent Systems” da Universidade da Califórnia (CML-UCI) possui centenas de conjuntos de dados, disponíveis gratuitamente nesse link: UCI Machine Learning Repository. Um dos conjuntos de dados mais utilizados é o iris data set, que contém as dimensões de pétalas (protegem partes reprodutoras da planta e atraem polinizadores) e sépalas (partes semelhantes a folhas que envolvem o botão da flor) de exemplares de três espécies de flores iris. Ele contém 3 classes (Iris Setosa, Iris Versicolour e Iris Virginica) de 50 instâncias cada. Uma classe é linearmente separável das outras duas; estas últimas NÃO são separáveis linearmente entre si. Aqui, o objetivo é classificar a planta conforme quatro características físicas (em cm): comprimento da sépala, largura da sépala, comprimento da pétala e largura da pétala.
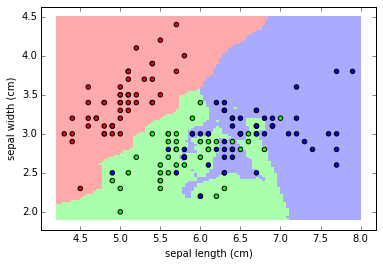
A figura acima ilustra a classificação usando k-NN (mapa de cores) para as instâncias com classes já informadas (pontos coloridos) considerando apenas o comprimento e largura da sépala (vermelho é virginica, verde é versicolor e azul é setosa).
Implementação em Python
Além de definir o conjunto de dados de treinamento e a métrica para calcular a distância entre os exemplos de treinamento, também deve-se definir o número de vizinhos mais próximos que serão considerados pelo algoritmo (o valor de K).
Não existe um valor único para o K (varia de acordo com a base de dados). Se K for muito pequeno, a classificação fica sensível a pontos de ruído; Se K for muito grande, a vizinhança pode incluir elementos de outras classes. Pode-se definir um valor inicial como a raiz quadrada do número de amostras e então ir chutando valores para ver qual K acerta mais, desde que K seja um número ímpar/primo.
O algoritmo k-NN consiste em, para cada nova amostra:
- Calcular a distância entre o exemplo desconhecido e o outros exemplos do conjunto de treinamento
- Identificar os K vizinhos mais próximos
- O rótulo da classe com mais representantes no conjunto definido no passo anterior será o escolhido (voto majoritário)
Esse algoritmo foi aplicado no script a seguir. São utilizados o “iris data set” (com 150 amostras), a distância Euclidiana como métrica e K = 13. O objetivo é classificar a classe da planta íris conforme as quatro dimensões fornecidas de suas flores. Uma parte das amostras (60%) é utilizada para fazer o treinamento e o restante serve para fazer o teste, que funciona da seguinte forma: o algoritmo faz a classificação e o resultado é comparado com seu valor de classe conhecido; se a classe prevista for a mesma que a observada, é registrado um acerto.
Como é retirada uma porcentagem dos dados para treinamento conforme a ordem das linhas, deve-se reordenar randomicamente as linhas, já que o arquivo original possui as linhas ordenadas por classe. Para isso, use o comando “cat iris.data | sort -R > iris.data2” no terminal Linux ou “random.shuffle(amostras)” logo após fechar o “for” de leitura do arquivo (nesse caso, cada vez que rodar o script os dados são rearranjado, atrapalhando outras comparações).
#!/usr/bin/python
# -*- coding: utf-8 -*-
# Implementação do k-NN para "iris data set"
import sys
import math
import random
######################### FUNÇÕES #########################
# Imprime informações sobre os dados de iris.data
def info_dataset(amostras, verbose=True):
if verbose:
print('Total de amostras: %d' % len(amostras))
rotulo1, rotulo2, rotulo3 = 0, 0, 0
for amostra in amostras:
if amostra[-1] == 'Iris-setosa':
rotulo1 += 1
elif amostra[-1] == 'Iris-versicolor':
rotulo2 += 1
elif amostra[-1] == 'Iris-virginica':
rotulo3 += 1
else:
print("nenhuma classificação!")
if verbose:
print('Total rotulo 1: %d' % rotulo1)
print('Total rotulo 2: %d' % rotulo2)
print('Total rotulo 3: %d' % rotulo3)
return [len(amostras), rotulo1, rotulo2, rotulo3]
# Distância Euclidiana
def dist_euclidiana(v1, v2):
dim, soma = len(v1), 0
# loop sem pegar a última coluna pq é a saída (dim - 1)
for i in range(dim - 1):
soma += math.pow(v1[i] - v2[i], 2)
return math.sqrt(soma)
# KNN propriamente dito
def knn(treinamento, nova_amostra, K):
dists, tam_treino = {}, len(treinamento)
# calcula a distância euclidiana das amostras de treinamento
for i in range(tam_treino):
d = dist_euclidiana(treinamento[i], nova_amostra)
dists[i] = d
# obtém as chaves (índices) dos k-vizinhos mais próximos
k_vizinhos = sorted(dists, key=dists.get)[:K]
# votação majoritária
qtd_rotulo1, qtd_rotulo2, qtd_rotulo3 = 0, 0, 0
for indice in k_vizinhos:
if treinamento[indice][-1] == 'Iris-setosa':
qtd_rotulo1 += 1
elif treinamento[indice][-1] == 'Iris-versicolor':
qtd_rotulo2 += 1
elif treinamento[indice][-1] == 'Iris-virginica':
qtd_rotulo3 += 1
# Imprimir/retornar classe com mais votos
if (qtd_rotulo1 > qtd_rotulo2 and qtd_rotulo1 > qtd_rotulo3):
#print('Classe 1')
return 'Iris-setosa'
elif (qtd_rotulo2 > qtd_rotulo1 and qtd_rotulo2 > qtd_rotulo3):
#print('Classe 2')
return 'Iris-versicolor'
elif (qtd_rotulo3 > qtd_rotulo1 and qtd_rotulo3 > qtd_rotulo2):
#print('Classe 3')
return 'Iris-virginica'
######################### PROGRAMA #########################
# Inicialização da lista de amostras
amostras = []
# Carregar dados de arquivo CSV com amostras
with open('iris.data2', 'r') as f:
#ler arquivo linha por linha
for linha in f.readlines():
# obter os atributos da amostra
atrib = linha.replace('\n','').split(',')
amostras.append([float(atrib[0]), float(atrib[1]), float(atrib[2]), float(atrib[3]), atrib[4]])
# Guardar totais de cada rótulo/classe
_, rotulo1, rotulo2, rotulo3 = info_dataset(amostras, verbose=False)
# Separar 60% dos dados para treinamento e o restante fica para testar
p = 0.6
treinamento, teste = [], []
cont = 1
max_rotulo1, max_rotulo2, max_rotulo3 = int(p*rotulo1), int(p*rotulo2), int(p*rotulo3)
total_rotulo1, total_rotulo2 , total_rotulo3 = 0, 0, 0
for amostra in amostras:
if cont <= (max_rotulo1 + max_rotulo2 + max_rotulo3):
treinamento.append(amostra)
if amostra[-1] == 'Iris-setosa' and total_rotulo1 < max_rotulo1:
total_rotulo1 += 1
elif amostra[-1] == 'Iris-versicolor' and total_rotulo2 < max_rotulo2:
total_rotulo2 += 1
elif amostra[-1] == 'Iris-virginica' and total_rotulo3 < max_rotulo3:
total_rotulo3 += 1
else:
teste.append(amostra)
cont += 1
# Testar com as amostras do conjunto de teste
acertos = 0
K = 13
for amostra in teste:
classe = knn(treinamento, amostra, K)
#print('%s X %s' % (amostra[-1], classe))
#sys.exit("fim de teste")
if amostra[-1] == classe:
acertos += 1
print('Total de treinamento: %d' % len(treinamento))
print('Total de testes: %d' % len(teste))
print('Total de acertos: %d' % acertos)
print('Porcentagem de acertos: %.2f%%' % (100 * acertos / len(teste)))
A saída revela o número de amostras utilizadas no treinamento, o total de testes realizados e o número de classificações acertadas (com exibição em porcentagem também):
$ python3 knn_iris.py Total de treinamento: 90 Total de testes: 60 Total de acertos: 57 Porcentagem de acertos: 95.00%
Nota-se que o modelo do tipo k-NN, implementado para classificar o tipo de flor conforme as dimensões da sépala e da pétala, consegue estimar bem a classe de novos dados (não utilizados no treinamento).
Implementação em Python scikit-learn
A scikit-learn (de SciPy Toolkit) é uma biblioteca de aprendizado de máquina de código aberto para a linguagem de programação Python, uma extensão do SciPy desenvolvida por terceiros e distribuída separadamente. É projetada para interagir com as bibliotecas Python numéricas e científicas, como a NumPy, que suporta arrays e matrizes multidimensionais e também possui maior desempenho para realizar operações matemáticas que demandam mais processamento. Para sua instalação no Python 3 (foi utilizado Python 3.5.2), execute os seguintes comandos no terminal Linux:
sudo apt-get install python3-pip # caso não tenha o pip instalado para python 3 sudo pip3 install scikit-learn
Para versões mais antigas de Linux, usar “sudo apt-get install python3-setuptools && sudo easy_install3 pip” no lugar da primeira linha.
Para instalar via conda, use:
conda install -c anaconda scikit-learn
O código apresentado anteriormente pode ficar mais sucinto e eficiente usando a biblioteca sklearn.neighbors.KNeighborsClassifier da scikit-learn e seus métodos. Veja como fica o código para as mesmas condições utilizadas no script anterior:
#!/usr/bin/python
# -*- coding: utf-8 -*-
# Implementação do k-NN com skLearn
import sys
from sklearn.neighbors import KNeighborsClassifier
# Inicialização da lista de amostras separada em entrada e saída (classes)
entradas, saidas = [], []
# Carregar dados de arquivo CSV com amostras
with open('iris.data2', 'r') as f:
#ler arquivo linha por linha
for linha in f.readlines():
# obter os atributos da amostra
atrib = linha.replace('\n','').split(',')
entradas.append([float(atrib[0]), float(atrib[1]), float(atrib[2]), float(atrib[3])])
saidas.append(atrib[4])
# Separar 60% dos dados para treinamento e o restante fica para testar
p = 0.6
limite = int(p * len(entradas))
# Chamar a função do skLearn para aplicar o k-NN com K = 13
knn = KNeighborsClassifier(n_neighbors=13)
# Ajustar o modelo usando "entradas" como dados de treinamento e "saidas" como valores-alvo
knn.fit(entradas[:limite], saidas[:limite])
# Previsão dos rótulos das classes para o restante da base de dados
rotulos_previstos = knn.predict(entradas[limite:])
# Contabilizar acertos para os dados de teste
acertos, indice_rotulo = 0, 0
for i in range(limite, len(entradas)):
if rotulos_previstos[indice_rotulo] == saidas[i]:
acertos += 1
indice_rotulo += 1
print('Total de treinamento: %d' % limite)
print('Total de testes: %d' % (len(entradas) - limite))
print('Total de acertos: %d' % acertos)
print('Porcentagem de acertos: %.2f%%' % (100 * acertos / (len(entradas) - limite)))
A saída deve ser a mesma do caso anterior.
Para estudo e previsão de séries temporais, existe o kNN-TSP (k-Nearest Neighbor – Time Series Prediction). Sua ideia consiste em, considerando os últimos n registros ocorridos, encontrar as subsequências de tamanho n que apresentaram comportamentos similares no passado. Com base nas informações dessas subsequências, é realizado o cálculo do valor futuro.
Fonte: curso Machine Learning e Data Science com Python da udemy.



One comment