Física nuclear

A Física nuclear é o ramo da física que estuda as propriedades, estrutura e comportamento do núcleo atômico, incluindo as forças que mantêm os prótons e nêutrons unidos, os processos de decaimento radioativo, e as reações nucleares, como a fissão e a fusão. Essa área envolve tanto investigações fundamentais sobre a natureza da matéria quanto aplicações práticas baseadas nas interações entre núcleos e partículas.

As aplicações práticas da física nuclear são vastas e impactam diversas áreas. Na medicina, destaca-se a medicina nuclear, que utiliza radioisótopos para diagnóstico por imagem (como o PET-Scan) e tratamentos oncológicos com radioterapia. Na indústria, técnicas nucleares são aplicadas no controle de qualidade, irradiação de alimentos, inspeção de soldas e análise de materiais. Além disso, a geração de energia elétrica por meio de reatores nucleares representa uma importante fonte alternativa de energia limpa e de alta densidade energética.

No Brasil, a física nuclear é regulamentada e desenvolvida por instituições como a Comissão Nacional de Energia Nuclear (CNEN), responsável pela fiscalização, regulamentação e promoção do uso seguro de tecnologias nucleares. O Instituto de Pesquisas Energéticas e Nucleares (IPEN), vinculado à CNEN e localizado em São Paulo, é um dos principais centros de pesquisa e produção de radioisótopos no país. A geração de energia nuclear é realizada principalmente pelas usinas de Angra 1 e Angra 2, operadas pela Eletronuclear, que compõem o complexo nuclear de Angra dos Reis, no Rio de Janeiro.

1. Fundamentos da física atômica e nuclear

A Física Atômica e Nuclear estuda a estrutura e o comportamento da matéria em escalas extremamente pequenas, focando nos átomos e seus núcleos. A matéria é composta por átomos, formados por um núcleo central (contendo prótons e nêutrons) e elétrons orbitando ao redor. Os modelos atômicos evoluíram historicamente: desde o modelo de Dalton (átomo indivisível), passando pelo modelo de Thomson (pudim de passas), Rutherford (núcleo denso e positivo), Bohr (órbitas quantizadas) até os modelos quânticos modernos (modelo de Schrödinger), que descrevem os elétrons em termos de funções de onda.

No nível nuclear, os modelos explicam propriedades como massa, estabilidade e decaimento radioativo. Interações nucleares são regidas por forças fortes e fracas, responsáveis por fenômenos como fusão e fissão nuclear. Para descrever matematicamente um núcleo, o problema fundamental seria resolver a equação de Schrödinger para um sistema de muitos corpos (todos os prótons e nêutrons do núcleo) interagindo entre si. No entanto, a equação de muitos corpos é extremamente complexa e não conhecemos o potencial de interação nucleon-nucleon de forma exata. Existem alguns modelos aproximados:

• Modelo de gás de Fermi: trata o núcleo como um conjunto de prótons e nêutrons que se movem livremente dentro de um potencial, obedecendo à estatística de Fermi-Dirac. Explica bem propriedades médias de núcleos pesados, como a energia de ligação por nucleon, mas não explica, por exemplo, a existência de números mágicos.
• Modelos coletivos: combinam movimentos coletivos dos núcleons (como rotações e vibrações do núcleo inteiro) com aspectos individuais dos nucleons. São mais usados para explicar fenômenos como estados excitados em núcleos deformados e transições nucleares.
• Modelo de camadas: assume que prótons e nêutrons estão em níveis discretos de energia (como elétrons em átomos), sujeitos a um potencial médio mais uma interação spin-órbita. Explica muito bem as propriedades de núcleos estáveis, a existência dos números mágicos (2, 8, 20, 28, 50, 82, 126, o que denuncia a existência de camadas), e várias características de momentos magnéticos e de quadrupolo dos núcleos.

O modelo da gota líquida, complementar aos listados, foi proposto para explicar as propriedades macroscópicas dos núcleos atômicos, especialmente a energia de ligação dos núcleos, a estabilidade dos núcleos e o processo de fissão nuclear. Ele trata o núcleo como se fosse uma gota de líquido: os nucleons (prótons e nêutrons) se comportam como moléculas de um líquido fortemente ligado, existe uma força de coesão (de curta distância) semelhante às forças intermoleculares, e há uma repulsão devido à carga elétrica dos prótons (repulsão coulombiana). A energia total do núcleo é dada pela fórmula semiempírica da massa (ou fórmula de Weizsäcker) – \( \delta(A, Z)\) é o termo de paridade (ou de emparelhamento), que depende se o número de prótons e nêutrons é par ou ímpar:

\(B(A, Z) = a_v A – a_s A^{2/3} – a_c \frac{Z^2}{A^{1/3}} – a_a \frac{(A – 2Z)^2}{A} + \delta(A, Z)\)

Em núcleos leves, o número de prótons Z e o número de nêutrons N são aproximadamente iguais. À medida que os núcleos ficam mais pesados, precisa ter mais nêutrons que prótons para compensar a repulsão elétrica entre os prótons (mas para núcleos mais leves, essa relação é bem próxima). A energia de ligação B mede o quão estável é o núcleo: quanto maior B, mais estável o núcleo. Se Z for muito diferente de A/2 (isto é, se tiver muito mais prótons ou nêutrons que o “ideal”), o núcleo se torna menos estável. Portanto, a máxima energia de ligação (maior estabilidade) ocorre quando Z≈A/2. Então adicionamos um termo corretivo proporcional a na fórmula da energia de ligação, chamado de termo de assimetria na fórmula de Weizsäcker: (A-2Z)²/A.

No modelo de camadas nuclear, queremos construir um potencial médio para descrever o movimento de um nucleon dentro do núcleo. O Potencial de Woods-Saxon é uma boa aproximação, pois o potencial real é nem infinitamente duro (poço esférico infinito) nem tão macio (oscilador harmônico tridimensional esférico). Para remover as degenerescência (diferentes estados físicos com a mesma energia) e explicar definitivamente os números mágicos, é essencial incluir outro termo com a interação spin-órbita. A energia de um estado passa a depender do momento angular total j (que combina l e s), e para cada l, o potencial define estados com paridade associada.

Para núcleos deformados ou muito afastados de números mágicos, modelos coletivos (gota líquida, rotações, vibrações) se tornam essenciais para descrever os níveis de energia. Assim, na prática, a descrição “real” da estrutura nuclear é uma mistura de comportamento de partículas individuais (modelo de camadas) e comportamento coletivo.

2. Estabilidade nuclear, energia de ligação, reações nucleares

A estabilidade de um núcleo atômico depende do equilíbrio entre as forças atrativas e repulsivas em seu interior. As partículas nucleares (prótons e nêutrons, chamadas genericamente de núcleons) estão sujeitas à força nuclear forte, que é atrativa em curtas distâncias e atua para manter o núcleo coeso, e à força eletrostática repulsiva entre os prótons. Quando há um balanço adequado entre o número de prótons e nêutrons, o núcleo é estável; do contrário, ele pode sofrer decaimento radioativo.

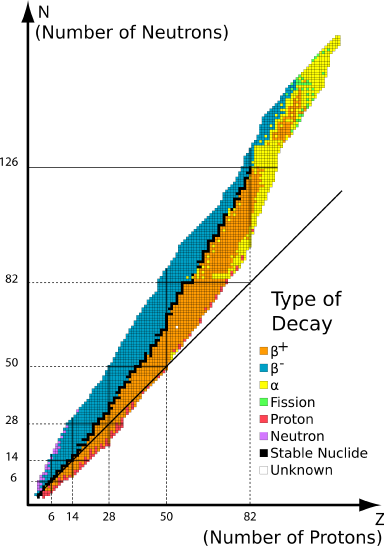
A energia de ligação nuclear é a quantidade de energia necessária para separar completamente um núcleo em seus núcleons. É também a energia liberada quando o núcleo é formado a partir desses núcleons. Essa energia é um indicativo da estabilidade do núcleo: quanto maior a energia de ligação por núcleon, mais estável é o núcleo. Núcleos com número de massa intermediário (como o ferro-56) possuem as maiores energias de ligação por núcleon, sendo os mais estáveis.

As reações nucleares ocorrem quando núcleos interagem entre si ou com partículas subatômicas, resultando na transformação de elementos e liberação (ou absorção) de energia. As principais reações nucleares incluem:

• Fissão nuclear: divisão de um núcleo pesado (como U-235 ou Pu-239) em núcleos menores, liberando grande quantidade de energia e nêutrons. É a base de reatores nucleares e armas nucleares.
• Fusão nuclear: combinação de núcleos leves (como isótopos de hidrogênio) formando um núcleo mais pesado, também com liberação de energia. É o processo que ocorre no Sol e em outras estrelas.
• Decaimentos radioativos: transformação espontânea de núcleos instáveis em núcleos mais estáveis, com emissão de partículas alfa, beta ou radiação gama.
• Reações induzidas: quando partículas (como nêutrons ou prótons) colidem com núcleos, provocando reações nucleares, como (n,γ), (n,α), (p,n), entre outras.

A conservação de energia, número de massa (A) e número atômico (Z), assim como o balanço de momento e energia cinética, são princípios fundamentais para a análise e classificação dessas reações.

3. Principais tipos de radiações nucleares

As radiações nucleares são emissões provenientes de processos de decaimento de núcleos instáveis ou de reações nucleares. Podem ser classificadas em partículas ou radiações eletromagnéticas, e diferem em natureza, energia, poder de penetração e efeitos biológicos.

Partículas Alfa (α)

• Constituem-se de 2 prótons e 2 nêutrons (núcleo de hélio-4).
• São emitidas por núcleos pesados (ex: urânio, rádio, polônio).
• Possuem baixa penetração (podem ser barradas por uma folha de papel ou pela pele) mas alto poder ionizante.
• O núcleo que emite uma partícula alfa tem sua massa reduzida em 4 unidades e o número atômico em 2.

Partículas Beta (β⁻)

• São elétrons de alta energia emitidos por núcleos com excesso de nêutrons.
• Resultam da conversão de um nêutron em um próton, com emissão de um elétron (β⁻) e um antineutrino.
• Têm penetração moderada (barradas por alumínio fino) e poder ionizante médio.
• O número atômico do núcleo aumenta em 1, sem alteração da massa.

Pósitrons (β⁺)

• Antipartículas do elétron, com mesma massa e carga positiva.
• Emitidos por núcleos com excesso de prótons, via conversão de um próton em nêutron, com emissão de um pósitron e um neutrino.
• Também possuem penetração moderada e colidem com elétrons, gerando aniquilação e emissão de fótons gama.

Raios Gama (γ)

• São radiações eletromagnéticas de altíssima energia, emitidas por núcleos excitados após processos de decaimento ou reações nucleares.
• Não têm massa nem carga, mas altíssimo poder de penetração (barrados apenas por materiais densos como chumbo ou concreto espesso).
• Baixo poder ionizante isoladamente, mas perigosos pela capacidade de atravessar tecidos humanos.

Nêutrons

• Emissões típicas de reações de fissão ou fontes isotópicas (ex: califórnio-252).
• Sem carga elétrica, o que confere grande poder de penetração, pois não são repelidos por núcleos atômicos.
• Interagem com núcleos, podendo causar reações nucleares secundárias ou ativação de materiais (tornando-os radioativos).
• Classificados por energia: térmicos (lentos), rápidos e ultra-rápidos.

4. Decaimento radioativo

Decaimento radioativo é o processo pelo qual núcleos instáveis se transformam espontaneamente em núcleos mais estáveis, emitindo radiação no processo. A meia-vida \( t_{1/2} \) é o tempo necessário para que metade dos núcleos de uma amostra radioativa decaia. A atividade A representa a taxa de decaimento, isto é, o número de desintegrações por unidade de tempo, sendo dada por:

\(A = \lambda N\)

onde:

• A é a atividade (em becquerel, 1 Bq = 1 desintegração por segundo; 1 curie (Ci) equivale a \(3,7 \times 10^{10} \) becquerels),
• \( \lambda \) é a constante de decaimento (em \(s^{-1}\)),
• N é o número de núcleos radioativos presentes.

A relação entre a constante de decaimento e a meia-vida é:

\(t_{1/2} = \frac{\ln 2}{\lambda}\)

Esse comportamento segue a lei do decaimento exponencial:

\(N(t) = N_0 e^{-\lambda t}\)

em que N(t) é o número de núcleos remanescentes no tempo t, e \( N_0 \) é o número inicial de núcleos.

5. Interação de radiação ionizante com a matéria

A radiação ionizante interage com a matéria principalmente por meio de processos que transferem energia aos elétrons dos átomos, podendo arrancá-los e formar íons. Para radiação eletromagnética (como raios X e gama), os principais mecanismos de interação com elétrons atômicos são:

Efeito Fotoelétrico

• O fóton incidente transfere toda sua energia a um elétron ligado (geralmente da camada K ou L), que é ejetado do átomo.
• Predomina para fótons de baixa energia (até ~100 keV) e em materiais de alto número atômico (Z).
• A energia cinética do elétron ejetado é: E = hv – E_ligação
• Essencial para a formação de imagem em radiografia e para blindagens contra raios X.

Efeito Compton

• O fóton colide com um elétron fracamente ligado ou livre, transferindo parte da energia e sofrendo desvio de trajetória com perda de energia (espalhamento).
• Predomina em materiais de baixo Z e para fótons com energia intermediária (~100 keV a vários MeV).
• Importante em ambientes com radiação dispersa e para o cálculo de dose absorvida em tecidos humanos.

Produção de Pares

• Ocorre quando um fóton com energia superior a 1,022 MeV (duas vezes a massa de repouso do elétron) interage com o campo elétrico do núcleo e se transforma em um par elétron-pósitron.
• O excesso de energia (se houver) se converte em energia cinética do par criado.
• Após a perda de energia, o pósitron se aniquila com um elétron, gerando dois fótons de 511 keV (radiação gama).
• Importante em física de altas energias e na tomografia por emissão de pósitrons (PET).

Espalhamento elástico

Ocorre quando uma partícula incide sobre um núcleo e não há mudança interna no núcleo nem na partícula — apenas uma troca de momento (energia cinética) e direção. Ou seja, o núcleo permanece no mesmo estado (sem excitação), e a partícula apenas sofre uma deflexão. Mudança de fase aqui significa mudança na função de onda da partícula espalhada (não na natureza da partícula ou do núcleo). Exemplos: espalhamento elástico de nêutrons em átomos leves (como hidrogênio ou carbono).

Reações nucleares (não-elásticas)

Acontecem quando o núcleo muda de estado ou há transformação na partícula ou no núcleo. Nesse caso, além da mudança de fase, ocorre também absorção de energia e modificação estrutural do sistema. Dentro das reações não-elásticas, temos subtipos:

• Núcleo composto: A partícula incidente é absorvida pelo núcleo, formando um sistema intermediário altamente excitado (o “núcleo composto”). Esse núcleo composto, depois de um breve tempo (~10^-16 s), decai liberando partículas ou fótons. O processo é estatístico: o núcleo “esquece” como foi formado, e o decaimento depende apenas da energia total. Exemplo: uma reação (n,γ), onde o nêutron é absorvido e depois o núcleo emite um fóton gama.
• Processos diretos: A interação entre a partícula e o núcleo é rápida e localizada, sem formação de núcleo composto. A partícula pode, por exemplo, arrancar um nêutron ou próton do núcleo de forma quase instantânea. É uma interação mais “simples” e dependente da geometria e da estrutura do núcleo. Exemplo: reações de espalhamento inelástico direto (p,p′) onde o núcleo é excitado e o próton sai.
• Reações ressonantes: Acontecem quando a energia da partícula incidente coincide com um nível de energia específico de excitação do núcleo composto. Isso gera uma grande probabilidade de reação (um “pico” nas seções de choque). É um processo de formação do núcleo composto, mas favorecido por uma energia específica (daí o nome ressonância). Exemplo: ressonâncias de nêutrons lentos no urânio-235.

6. Atenuação e absorção da radiação na matéria

Quando radiações ionizantes atravessam a matéria, parte de sua energia é transferida para o meio por meio de interações com os átomos e elétrons, resultando em atenuação e possível absorção total da radiação.

Atenuação

É a redução da intensidade da radiação ao atravessar um material, devida à soma dos processos de absorção e espalhamento. Para radiações fotônicas (raios X e gama), a atenuação segue a lei exponencial:

\(I = I_0 e^{-\mu x} \)

onde:

• I é a intensidade da radiação após atravessar o material,
• \( I_0 \) é a intensidade inicial da radiação,
• \( \mu \) é o coeficiente linear de atenuação do material (em \(cm^{-1}\), depende do material e da energia da radiação),
• x é a espessura do material (em cm).

Outro parâmetro importante é a camada semirredutora (Half-Value Layer – HVL), que é a espessura necessária para reduzir a intensidade da radiação à metade. Para materiais diferentes, a HVL varia significativamente.

Absorção

É o processo no qual a energia da radiação é totalmente depositada no meio material, geralmente por ionizações e excitações. No caso de radiação corpuscular (como partículas alfa e beta), a absorção é total após um certo alcance, diferente da radiação gama, que apenas sofre atenuação exponencial.

Blindagem

Consiste no uso de materiais apropriados para reduzir a exposição à radiação. A escolha do material depende do tipo de radiação:

• Partículas alfa: blindagem simples, como papel ou a própria epiderme.
• Partículas beta: plásticos, acrílicos ou alumínio (evita-se o uso de materiais de alto Z para evitar geração de radiação bremsstrahlung).
• Raios gama e X: requerem materiais densos como chumbo, aço, ou concreto.
• Nêutrons: requerem materiais com hidrogênio (ex: parafina, água) para moderação, e posteriormente materiais absorvedores (como boro ou cádmio).

O projeto de blindagens exige conhecimento dos espectros de energia da radiação e das propriedades do material, garantindo segurança radiológica e conformidade com normas técnicas.

7. Efeitos biológicos da radiação ionizante

A radiação ionizante pode causar efeitos significativos nos sistemas biológicos, especialmente ao interagir com moléculas fundamentais como o DNA. Esses efeitos dependem do tipo e energia da radiação, da dose absorvida, da taxa de exposição e da sensibilidade dos tecidos.

Mecanismos de interação

• Ação direta: a radiação interage diretamente com moléculas do DNA, quebrando ligações químicas.
• Ação indireta: mais comum, envolve a ionização da água (principal componente celular), formando radicais livres altamente reativos (ex: OH•), que danificam componentes celulares.

Efeitos determinísticos (não estocásticos)

• Ocorrem acima de um limiar de dose e sua gravidade aumenta com a dose.
• Exemplos: queimaduras, catarata, esterilidade, depressão da medula óssea, síndrome aguda da radiação (náuseas, vômitos, hemorragias).
• Manifestam-se em curto prazo após exposição intensa.

Efeitos estocásticos

• Não há limiar de dose conhecido; a probabilidade de ocorrência aumenta com a dose, mas a gravidade é independente da dose.
• Exemplos: câncer induzido por radiação, mutações genéticas hereditárias.
• Podem se manifestar anos após a exposição.

Fatores que influenciam os efeitos biológicos

• Tipo de radiação (alfa > beta > gama, em termos de efeito biológico por unidade de dose).
• Dose absorvida (medida em Gray – Gy).
• Equivalente de dose (considera o tipo de radiação; medida em Sievert – Sv).
• Taxa de dose e exposição acumulada.
• Idade, sexo, estado fisiológico e radiossensibilidade do tecido.

A compreensão desses efeitos fundamenta a necessidade de limites de exposição ocupacional, princípios de proteção radiológica (justificação, otimização e limitação), e o uso de dosimetria pessoal e ambiental.

8. Proteção radiológica

A proteção radiológica tem como objetivo principal proteger indivíduos, trabalhadores e o público em geral contra os riscos potenciais associados à exposição à radiação ionizante, garantindo que os benefícios de sua utilização superem os danos potenciais. Baseados nas recomendações da Comissão Internacional de Proteção Radiológica (ICRP) e adotados no Brasil pela CNEN (Comissão Nacional de Energia Nuclear), os princípios fundamentais são:

• Justificação – Nenhuma prática que envolva exposição à radiação deve ser adotada a menos que produza mais benefício do que dano.
• Otimização (Princípio ALARA – As Low As Reasonably Achievable) – As exposições devem ser mantidas tão baixas quanto razoavelmente exequível, considerando aspectos sociais, econômicos e tecnológicos.
• Limitação de dose – A exposição de indivíduos deve estar abaixo dos limites estabelecidos por norma, para evitar efeitos determinísticos e reduzir a probabilidade de efeitos estocásticos.

Grandezas radiológicas e unidades

• Exposição (X): Quantifica a ionização produzida no ar por fótons. Unidade: C/kg (coulomb por quilograma). Unidade antiga: Roentgen (R).
• Dose Absorvida (D): Quantidade de energia depositada por radiação em um meio. Unidade SI: Gray (Gy). 1 Gy = 1 J/kg.
• Dose Equivalente (H): Leva em conta o tipo de radiação, usando o fator de ponderação da radiação (wᵣ) H = D⋅wᵣ Unidade: Sievert (Sv). Ex: para radiação alfa, wᵣ = 20; para fótons e elétrons, wᵣ = 1.
• Dose Efetiva (E): Soma ponderada das doses equivalentes recebidas pelos diferentes tecidos, usando fatores de ponderação tecidual (wₜ). Representa o risco global de efeitos estocásticos para o corpo inteiro. Unidade: Sievert (Sv).

A CNEN estabelece os limites de dose por meio da Norma CNEN NN 3.01 – Diretrizes Básicas de Proteção Radiológica, em consonância com padrões internacionais (ICRP, IAEA). Os principais limites para exposição ocupacional são:

Região do Corpo / Grupo	Trabalhadores	Público em Geral
Dose efetiva anual	Até 20 mSv/ano (média em 5 anos) Máximo de 50 mSv em um único ano	1 mSv/ano Exceções pontuais: até 5 mSv em um único ano
Cristalino	20 mSv/ano (média) Máximo de 50 mSv em um único ano	Até 15 mSv/ano
Pele, mãos e pés	500 mSv/ano	50 mSv/ano

Além disso, a norma exige:

• monitoramento individual e ambiental,
• uso de dosímetros e equipamentos de proteção individual (EPIs),
• classificação de áreas (controlada, supervisionada),
• treinamento contínuo de trabalhadores expostos,
• implementação de programas de garantia da qualidade e segurança operacional.

A aplicação rigorosa desses princípios é essencial para garantir operações seguras em instalações nucleares, médicas, industriais e laboratoriais que utilizam fontes de radiação ionizante.

9. Instrumentação nuclear

A instrumentação nuclear abrange os dispositivos utilizados para detectar, medir e caracterizar radiações ionizantes. Diferentes tipos de detectores são escolhidos conforme o tipo de radiação, faixa de energia, sensibilidade desejada e aplicação específica.

Detectores Gasosos

Baseiam-se na ionização do gás dentro de uma câmara ao ser atravessado por radiação. Os pares íon-elétron gerados são coletados por um campo elétrico. Conforme a tensão aplicada, os detectores gasosos operam em diferentes regiões:

• Região de ionização: corrente proporcional ao número de pares formados (ex: câmara de ionização).
• Região proporcional: a ionização inicial desencadeia avalanches secundárias (ex: contador proporcional).
• Região Geiger-Müller: avalanche total independente da energia da radiação incidente (ex: tubo Geiger-Müller).

São úteis para contagem e monitoramento, mas têm resolução energética limitada.

Detectores de Cintilação

Baseiam-se na emissão de luz (cintilação) por certos materiais quando atingidos por radiação ionizante. Essa luz é convertida em sinal elétrico por um fotomultiplicador (PMT) ou fotodiodo.

• Materiais cintiladores comuns: NaI(Tl), CsI, plastificantes e líquidos orgânicos.
• Vantagens: alta eficiência, resposta rápida, boa sensibilidade.
• Amplamente usados em espectrometria gama, medicina nuclear e segurança.

Detectores de Semicondutores

Funcionam com base na geração de pares elétron-lacuna quando partículas ionizantes atravessam o material semicondutor (ex: silício ou germânio).

• Exemplo clássico: detector de germânio hiperpuro (HPGe), com alta resolução energética para espectrometria gama.
• Vantagens: excelente resolução energética, resposta rápida.
• Desvantagem: alguns requerem operação criogênica (ex: HPGe com nitrogênio líquido).

Eficiência dos Detectores

A eficiência de um detector é a razão entre o número de eventos detectados e o número real de eventos incidentes: Eficiência = contagens registradas / partículas incidentes.

• Eficiência absoluta: considera a taxa real de emissões da fonte.
• Eficiência relativa: compara com detectores padrão.
• Fatores influentes: geometria, blindagem, tipo de radiação, material do detector.

Equilíbrio Eletrônico Local (EEL)

Refere-se à condição onde o número de partículas carregadas que entram em um volume é igual ao número que sai. É fundamental em dosimetria para garantir que a energia depositada seja proporcional à energia absorvida. O EEL é geralmente alcançado em tecidos a uma certa profundidade após o início da interação da radiação.

Estatística da Contagem da Radiação

A detecção de radiação é um processo estocástico, e os eventos seguem a distribuição de Poisson:

• A média m é igual à variância (desvio padrão ao quadrado)
• O desvio padrão das contagens é a raiz da média
• Para grandes contagens, a distribuição tende à gaussiana.

Esses conceitos são essenciais para avaliar a incerteza de medidas, definir níveis de confiança e estimar limites de detecção.

10. Eletrônica nuclear

A eletrônica nuclear é o conjunto de circuitos e sistemas eletrônicos responsáveis pelo processamento dos sinais elétricos gerados pelos detectores de radiação. Esses sistemas são essenciais para adquirir, analisar e interpretar dados de eventos nucleares com precisão.

• Sistemas Analógicos: Operam com sinais contínuos. Eram amplamente utilizados antes da popularização da eletrônica digital. Os sinais do detector são amplificados, moldados e enviados a um analisador de amplitude (ou analisador monocanal) que seleciona pulsos dentro de uma faixa energética.
• Sistemas Digitais: Realizam a digitalização do sinal (conversão A/D – analógico para digital) logo após a pré-amplificação, permitindo processamento flexível por software. Permitem aquisição simultânea de espectros, correções em tempo real, e algoritmos de resolução e calibração mais avançados.

Os amplificadores nucleares são usados para adaptar o sinal do detector às características exigidas pelos analisadores. Os principais tipos incluem:

• Pré-amplificador: localizado junto ao detector, amplifica e preserva a integridade do sinal original.
• Amplificador linear: molda o pulso para análise posterior (melhora a razão sinal/ruído).
• Amplificador de pulso: usado para criar pulsos com formas específicas (altura proporcional à energia detectada).

A estabilidade e a linearidade dos amplificadores são essenciais para garantir boa resolução espectral.

Espectro Energético das Radiações

Quando partículas ionizantes interagem com o detector, geram sinais elétricos proporcionais à energia depositada. A análise desses sinais permite a construção de um espectro energético, que é um histograma da frequência de pulsos versus sua altura (ou energia correspondente).

• Picos: indicam partículas ou fótons com energia bem definida (ex: emissão gama específica).
• Contínuo: pode indicar espalhamento (ex: efeito Compton).

O estudo do espectro permite identificar radionuclídeos e quantificar atividade.

• Análise Monocanal (MCA analógico simples): Permite selecionar uma janela de energia, contando apenas pulsos cuja altura (energia) esteja dentro de uma faixa. Útil para detecção seletiva ou monitoração.
• Analisador Multicanal (MCA): Armazena pulsos em centenas ou milhares de canais que representam diferentes faixas energéticas, permitindo a aquisição de espectros completos em tempo real.

Componentes principais:

• Conversor analógico-digital (ADC)
• Memória para contagem em canais
• Interface com computador

A resolução de um sistema de detecção nuclear mede sua capacidade de distinguir picos energéticos próximos. É definida como:

\(\text{Resolução (FWHM)} = \frac{\Delta E}{E} \times 100\%\)

onde:

• \(\Delta E\) é a largura total do pico à meia-altura (Full Width at Half Maximum),
• E é a energia central (ou do pico) correspondente.

Essa fórmula expressa a resolução em percentual, e quanto menor o valor, melhor a resolução do sistema de detecção.

• Baixa resolução: espectros mais “largos”, difícil separar energias próximas.
• Alta resolução: espectros mais nítidos, fácil identificação de radionuclídeos.

A resolução depende do detector, da eletrônica associada (ganho, ruído, estabilidade) e da qualidade da calibração do sistema.

11. Confiabilidade de processos de medição

A metrologia é essencial para garantir a qualidade e a rastreabilidade das medições em laboratórios científicos, industriais e de controle regulatório. Este tópico abrange os princípios fundamentais da medição e os critérios normativos que asseguram a confiabilidade dos resultados.

• Exatidão (acurácia): grau de concordância entre o valor medido e o valor verdadeiro ou aceito como referência.
• Precisão: grau de concordância entre medições repetidas sob as mesmas condições. Alta precisão não implica necessariamente alta exatidão.

Um sistema pode ser preciso (resultados próximos entre si) e não exato (distantes do valor verdadeiro), e vice-versa.

• Erros aleatórios: variam imprevisivelmente entre medições. Ex: ruído eletrônico, flutuação ambiental. Podem ser reduzidos com repetição e tratamento estatístico.
• Erros sistemáticos: ocorrem de forma consistente, tendendo a desviar o valor na mesma direção. Ex: instrumento mal calibrado, interferência constante. Devem ser identificados e corrigidos.

Toda medição possui uma margem de incerteza, que expressa a confiança no resultado. Ela pode ser:

• Tipo A: avaliada por análise estatística (repetibilidade).
• Tipo B: baseada em estimativas, especificações do instrumento, experiência anterior.

A incerteza expandida é frequentemente usada para expressar resultados com nível de confiança (ex: 95%):

\(\text{Incerteza expandida} = k \cdot u_c\)

Onde \(u_c\) é a incerteza combinada e k é o fator de abrangência.

Calibração é o processo de comparar um instrumento com um padrão de referência reconhecido, a fim de determinar erros sistemáticos e aplicar correções.

• Envolve instrumentos de referência rastreáveis ao Sistema Internacional de Unidades (SI).
• Deve seguir procedimentos documentados e repetir-se em intervalos regulares.
• A calibração pode gerar certificados, incluindo incerteza associada e condição do equipamento.

Curva de Calibração é um gráfico que relaciona a resposta do sistema de medição (ex: sinal elétrico, contagem, intensidade) com valores conhecidos de uma grandeza física (ex: energia, concentração, atividade).

• Utilizada para converter sinais de saída em valores físicos interpretáveis.
• A curva pode ser linear ou não linear, dependendo da aplicação.
• A regressão linear é frequentemente utilizada para ajustar os dados experimentais.

Técnicas de Medições Diretas e Indiretas

• Medições diretas: obtêm-se diretamente os valores da grandeza de interesse com instrumentos apropriados. Ex: medir comprimento com régua.
• Medições indiretas: obtêm-se valores a partir de outras grandezas relacionadas por equações. Ex: calcular densidade pela razão entre massa e volume.

A seleção do método influencia a incerteza final.

A confiabilidade refere-se à reprodutibilidade, rastreabilidade e robustez das medições. Para ser confiável, um processo deve:

• Estar sob controle metrológico.
• Ter operadores treinados.
• Utilizar equipamentos calibrados e bem mantidos.
• Aplicar boas práticas laboratoriais e estatísticas.

Norma ABNT NBR ISO/IEC 17025

Esta norma estabelece os requisitos gerais para a competência de laboratórios de ensaio e calibração. Alguns pilares:

• Gestão da qualidade: controle documental, ações corretivas/preventivas, auditorias internas.
• Gestão técnica: rastreabilidade das medições, validação de métodos, garantia da qualidade dos resultados.
• Pessoal qualificado: operadores e analistas treinados e competentes.
• Ambiente de medição: controle das condições ambientais.
• Equipamentos: manutenção, calibração regular, registros.

A conformidade com a NBR ISO/IEC 17025 é pré-requisito para acreditação de laboratórios, garantindo confiança em resultados técnicos perante órgãos reguladores e clientes.

Exercício resolvidos

1. O isótopo radioativo Cobalto-60 tem meia-vida de aproximadamente 5,27 anos. Uma amostra inicial possui 80 g desse material.

a) Quantas meias-vidas se passaram nesse intervalo de tempo?

b) Qual será a massa restante de Cobalto-60 após 15,81 anos?

c) Qual a fração da massa que já decaiu?

Resolução

a) Fórmula do cálculo da massa restante após o tempo t:

\(m(t) = m_0 \cdot \left(\frac{1}{2}\right)^{t/T_{1/2}}\)

Onde:

• m(t) = massa após o tempo $t$
• \(m_0\) = 80 g (massa inicial)
• \(T_{1/2}\) = 5,27 anos (meia-vida)
• t = 15,81 anos

Isolando n e substituindo as constantes:

\(n = \frac{t}{T_{1/2}} = \frac{15{,}81}{5{,}27} = 3\)

Ou seja, 3 meias-vidas se passaram.

b) Cálculo da massa restante:

\(m(t) = 80 \cdot \left(\frac{1}{2}\right)^3 = 80 \cdot \frac{1}{8} = 10 \, \text{g}\)

c) A massa que já decaiu é:

\(m_{\text{decaída}} = m_0 – m(t) = 80 – 10 = 70 \, \text{g}\)

Fração decaída:

\(\text{Fração decaída} = \frac{70}{80} = 0{,}875 = 87{,}5\%\)

2. Um radionuclídeo tem uma meia-vida de 10 horas. Uma amostra contém inicialmente 2,0 µCi (microcuries) de atividade.

a) Qual será a atividade da amostra após 30 horas?

b) Qual a fração da atividade original que ainda resta após esse tempo?

c) Após quanto tempo a atividade será reduzida a 12,5% da inicial?

Resolução

a) A atividade radioativa decresce da mesma forma que a massa:

\(A(t) = A_0 \cdot \left(\frac{1}{2}\right)^{t/T_{1/2}}\)

Onde:

• A(t) = atividade no tempo $t$
• \(A_0\) = 2,0 µCi (atividade inicial)
• \(T_{1/2}\) = 10 h
• t = 30 h

Calculando o número de meias-vidas:

\(n = \frac{t}{T_{1/2}} = \frac{30}{10} = 3 \text{ meias-vidas}\)

Calculando a atividade:

\(A(t) = 2{,}0 \cdot \left(\frac{1}{2}\right)^3 = 2{,}0 \cdot \frac{1}{8} = 0{,}25 \, \mu\text{Ci}\)

b) Fração da atividade restante:

\(\text{Fração restante} = \frac{A(t)}{A_0} = \frac{0{,}25}{2{,}0} = 0{,}125 = 12{,}5\%\)

c) Queremos encontrar t tal que:

\(\frac{A(t)}{A_0} = 0{,}125 = \left(\frac{1}{2}\right)^n\)

Sabemos que:

\(0{,}125 = \left(\frac{1}{2}\right)^3 \Rightarrow n = 3\)

\(t = n \cdot T_{1/2} = 3 \cdot 10 = 30 \, \text{h}\)

3. A taxa de dose na superfície de um gerador de 99mTc é de 160 μSv/h. Considerando apenas a emissão do 99mTc, assinale a alternativa que expressa CORRETAMENTE a espessura de blindagem adicional de chumbo que reduziria a taxa de dose para 20 μSv/h? Obs.: camada semi-redutora (HVL) para 99mTc = 0,7 mm de chumbo.

Resolução

A redução da dose por camadas semi-redutoras (HVL) é dada por:

\(D = D_0 \cdot \left(\frac{1}{2}\right)^n\)

Onde:

• \(n = \frac{x}{\text{HVL}}\) = número de camadas semi-redutoras (com x em mm)
• D = 20 μSv/h (dose desejada após blindagem)
• \(D_0\) = 160 μSv/h (dose inicial)

Calculando a razão entre as doses:

\(\frac{D}{D_0} = \frac{20}{160} = \frac{1}{8}\)

Igualando com a fórmula da atenuação:

\(\left(\frac{1}{2}\right)^n = \frac{1}{8} \Rightarrow n = 3 \)

Ou seja, são necessárias 3 camadas semi-redutoras.

Calculando a espessura total:

\(x = n \cdot \text{HVL} = 3 \cdot 0{,}7 \, \text{mm} = 2{,}1 \, \text{mm} = 0{,}21 \, \text{cm}\)

4. Considere a seguinte equação nuclear incompleta para um decaimento radioativo:

\(^{220}_{88}X \rightarrow x\, ^4_2\alpha + y\, ^0_{-1}\beta + ^{208}_{86}Y\)

Quais os valores de x e de y?

Resolução

Queremos descobrir os valores de x (número de partículas alfa) e y (número de partículas beta menos).

Pela conservação do número de massa (A), a massa antes do decaimento é:

\(A_{\text{inicial}} = 220\)

Após o decaimento, a massa é:

\(A_{\text{final}} = x \cdot 4 + y \cdot 0 + 208 = 4x + 208\)

Igualando:

\(220 = 4x + 208 \Rightarrow 4x = 12 \Rightarrow x = 3\)

Pela conservação do número atômico (Z):

\(Z_{\text{inicial}} = 88\)

\(Z_{\text{final}} = x \cdot 2 + y \cdot (-1) + 86 = 2x – y + 86\)

Substituindo x = 3:

\(88 = 2 \cdot 3 – y + 86 \Rightarrow 88 = 6 – y + 86 \Rightarrow 88 = 92 – y \Rightarrow y = 4\)